题目内容
【题目】如图,直线y=x+1与x,y轴交于点A,B,直线y=-2x+4与x,y轴交于点D,C,这两条直线交于点E.
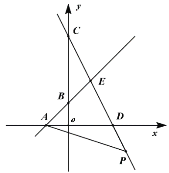
(1)求E点坐标;
(2)若P为直线CD上一点,当△ADP的面积为9时,求P的坐标.
【答案】(1)点E的坐标为(1,2);(2)点 P的坐标为(-1,6)或(5,-6).
【解析】
(1)把y=x+1与y=-2x+4联立组成方程组,解方程组求得x、y的值,即可求得点E的坐标;(2)先求得点A的坐标为(-1,0)、点D的坐标为(2,0),可得AD=3,根据△ADP的面积为9求得△ADP边AD上的高为6,可得点P的纵坐标为6,再分当点P在y轴的上方时和当点P在y轴的下方时两种情况求点P的坐标即可.
(1)由题意得,![]() ,
,
解得,![]() ,
,
∴点E的坐标为(1,2);
(2)∵直线y=x+1与x交于点A,直线y=-2x+4与x交于点D,
∴A(-1,0),D(2,0),
∴AD=3,
∵△ADP的面积为9,
∴△ADP边AD上的高为6,
∴点P的纵坐标为6,
当点P在y轴的上方时,-2x+4=6,
解得x=-1,
∴P(-1,6);
当点P在y轴的下方时,-2x+4=-6,
解得x=5,
∴P(5,-6);
综上,当△ADP的面积为9时,点 P的坐标为(-1,6)或(5,-6).

练习册系列答案
相关题目