��Ŀ����
����Ŀ��ij������Ʒ�̵�Ϊ�˽�5�·ݵ�����������Ա��¸�����Ʒ������������е��飬��������Ľ�����Ƴ�����������������ͳ��ͼ
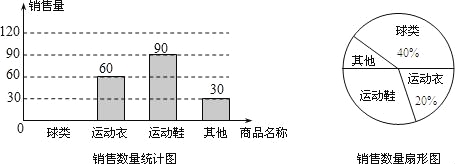
��1�������ͼ���ṩ����Ϣ��������ͼ����������
��2�����̵�����5�·�������Ʒ��������������������Ʒ����������������������Ԥ��ǡ����������3600Ԫ���蹺������x��������y����������Ľ��ۺ��ۼ������
��� | ���� | ���� | ���� |
���ۣ���λ��Ԫ/���� | 50 | 30 | 20 |
Ԥ�ۼۣ���λ��Ԫ/���� | 70 | 45 | 25 |
���y��x֮��ĺ�����ϵʽ��
��3���ڣ�2���еĽ��ۺ��ۼ۵������£���ʵ�������Ԥ���������۳���60����������ͻ��������
��������������������������ȫ���۳������Ԥ������P��Ԫ����x�������ĺ�����ϵʽ��
�����Ԥ����������ֵ����д����ʱ��������������ٸ���
���𰸡�(1)���𰸼�������(2)��y=��3x+120��(3)������P=��15x+1800���������ֵΪ1500Ԫ������20��������60��������40��
��������
���������(1)���������ͳ��ͼ�еı�����ϵ�����������������ٲ�����������ͳ��ͼ���ɣ�(2)���ú�x��y�Ĵ���ʽ��ʾ��������Ĺ��������ٸ���������Ľ����3600Ԫ�������г�����x��y�ĵ�ʽ�������ɵó����ۣ� (3)��������������=��������+��������+�������������ɵó�P����x�ĺ�����ϵʽ���������������۳���60����������ͻ�������������г�����x��һԪһ�β���ʽ���ⲻ��ʽ���ɵó�x��ȡֵ��Χ���ٸ���һ�κ��������ʼ��ɽ����ֵ���⣮
���������(1)���������������Ϊ60��![]() =120������������������ͳ��ͼ����ͼ��ʾ��
=120������������������ͳ��ͼ����ͼ��ʾ��
(2)���������֪������120��x��y��������50x+30y+20��120��x��y��=3600��
�����ã�y=��3x+120��
(3)����������ã�P=20x+15y+5��120��x��y���������ã�P=��15x+1800��
�����������в���ʽ����120��3x��60�� ��ã�x��20�� ��x�ķ�ΧΪx��20����xΪ������
��P��x��һ�κ�������15��0����P��x���������С��
����xȡ��Сֵ20ʱ��P�����ֵ�����ֵΪ1500Ԫ����ʱ��������20��������60��������40����


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д�