题目内容
【题目】用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2+2ab+a.
如:1☆3=1×32+2×1×3+1=16.
(1)求(﹣2)☆3的值;
(2)若( ![]() ☆3)☆(﹣
☆3)☆(﹣ ![]() )=8,求a的值;
)=8,求a的值;
(3)若2☆x=m,( ![]() x)☆3=n(其中x为有理数),试比较m,n的大小.
x)☆3=n(其中x为有理数),试比较m,n的大小.
【答案】
(1)解:(﹣2)☆3=﹣2×32+2×(﹣2)×3+(﹣2)
=﹣18﹣12﹣2
=﹣32
(2)解: ![]() ☆3=
☆3= ![]() ×32+2×
×32+2× ![]() ×3+
×3+ ![]() =8(a+1)
=8(a+1)
8(a+1)☆(﹣ ![]() )
)
=8(a+1)×(﹣ ![]() )2+2×8(a+1)×(﹣
)2+2×8(a+1)×(﹣ ![]() )+8(a+1)
)+8(a+1)
=8
解得:a=3
(3)解:由题意m=2x2+2×2x+2=2x2+4x+2,
n= ![]() ×32+2×
×32+2× ![]() x×3+
x×3+ ![]() =4x,
=4x,
所以m﹣n=2x2+2>0.
所以m>n
【解析】(1)根据已知条件新运算:对于任意有理数a和b,规定a☆b=ab2+2ab+a,把a=1,b=3代入求解;(2)根据题意列出关于a的方程求解;(3)根据(1)的运算求出2☆x=m,( ![]() x)☆3=n的值,再比较大小。
x)☆3=n的值,再比较大小。

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
【题目】下表是初二年级50名同龄女生身高数据:
身高/cm | 146 | 151 | 153 | 154 | 156 | 157 | 158 | 159 | 160 |
人数 | 1 | 2 | 2 | 2 | 3 | 4 | 8 | 4 | 4 |
身高/cm | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 169 | |
人数 | 2 | 4 | 3 | 2 | 3 | 4 | 1 | 1 |
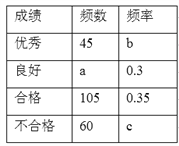
(1)根据下表的分组方法进行数据整理,补全频数分布表:
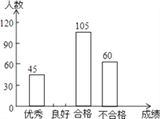
(2)根据分布表画出频数分布直方图.
(3)观察频数分布表和频数分布直方图回答问题:为了参加广播操比赛,老师打算从以上50名女生中挑选30名队员。为了让参赛队员的身高比较整齐,老师应该选择身高在什么范围内的同学呢?请写出答案并简述理由.