��Ŀ����
����Ŀ��������̽����
��ͼ�������У���ABC�����Ϊa.

(1)��ͼ�٣��ӳ���ABC�ı�BC����D��ʹCD��BC������DA������ACD�����ΪS1����S1��________(�ú�a��ʽ�ӱ�ʾ)��
(2)��ͼ�ڣ��ӳ���ABC�ı�BC����D���ӳ���CA����E��ʹCD��BC��AE��CA������DE������DEC�����ΪS2����S2��________(�ú�a��ʽ�ӱ�ʾ)����˵��������
(3)��ͼ�ۣ���ͼ�ڵĻ������ӳ�AB����F��ʹBF��AB������FD��FE���õ���DEF������Ӱ���ֵ����ΪS3����S3��________(�ú�a��ʽ�ӱ�ʾ)��
���𰸡���1��a����2��2a����3��6a.
�������������������1������A��AH��BD��H����ͼ1�����ڡ�ACD���ABC����ȡ�����ͬ��������ǵ������ȣ�������Խ����
��2������AD����ͼ2��ͬ��1���������EAD��������Ϳɽ�����⣻
��3����ͼ3��ͬ��2���������EAF�͡�FBD�������������Խ��.
�����������1������A��AH��BD��H����ͼ1��
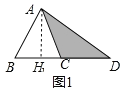
��BC=CD��S��ABC=![]() BCAH=a��S��ACD=
BCAH=a��S��ACD=![]() CDAH��
CDAH��
��S1=S��ACD=S��ABC=a��
�ʴ�Ϊa��
��2������AD����ͼ2��
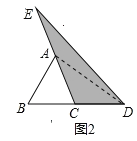
ͬ���ɵ�S��EAD=S��ACD=S��ABC=a��
��S2=S��ECD=a+a=2a��
�ʴ�Ϊ2a��
��3��ͬ��2���ɵ�
S��FBD=S��EAF=S��ECD=2a��
��S3=6a��
�ʴ�Ϊ6a

 ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д� С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д�