Question

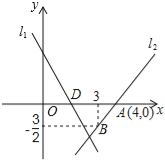
【题目】如图，直线l1的解析表达式为：y=﹣3x+3，且l1与x轴交于点D，直线l2经过点A、B，直线l1，l2交于点C．

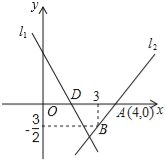
（1）求点D的坐标；

（2）求直线l2的解析表达式；

（3）求△ADC的面积；

（4）在l2上存在异于点C的另一点P，使得△ADP与△ADC面积相等，求点P的坐标．

Answer 1

【答案】（1）D（1，0）；（2）；（3）；（4）P（6，3）．

【解析】

试题（1）已知l1的解析式，令y=0求出x的值即可；

（2）设l2的解析式为y=kx+b，由图联立方程组求出k，b的值；

（3）先解方程组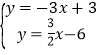，确定C（2，﹣3），再利用x轴上点的坐标特征确定D点坐标，然后根据三角形面积公式求解；

（4）由于△ADP与△ADC的面积相等，根据三角形面积公式得到点P与点C到AD的距离相等，则P点的纵坐标为3，对于函数y=x﹣6，计算出函数值为3所对应的自变量的值即可得到P点坐标．

试题解析：解：（1）∵y=﹣3x+3，

∴令y=0，得﹣3x+3=0，

解得x=1，

∴D（1，0）；

（2）设直线l2的解析表达式为y=kx+b，

由图象知：x=4，y=0；x=3，y=﹣，

代入表达式y=kx+b，

得，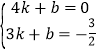

解得，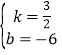

所以直线l2的解析表达式为y=x﹣6；

（3）由，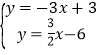

解得，

∴C（2，﹣3），

∵AD=3，

∴S△ADC=×3×|﹣3|=；

（4）因为点P与点C到AD的距离相等，

所以P点的纵坐标为3，

当y=3时，x﹣6=3，解得x=6，

所以P点坐标为（6，3）．