题目内容
【题目】(8分)在ΔABC中,AB=AC
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC=__________
(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC=__________
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示: _____________
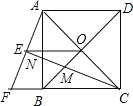
(4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由.



【答案】(1)15° (2)20°(3)∠BAD=2∠EDC(4)是,证明见解析.
【解析】试题分析:(1)等腰三角形三线合一,所以∠DAE=30°,又因为AD=AE,所以∠ADE=∠AED=75°,所以∠DEC=15°.
(2)同理,易证∠ADE=70°,所以∠DEC=20°.
(3)通过(1)(2)题的结论可知,∠BAD=2∠EDC(或∠EDC=![]() ∠BAD).
∠BAD).
(4)由于AD=AE,所以∠ADE=∠AED,根据已知,易证∠BAD+∠B=2∠EDC+∠C,而B=∠C,所以∠BAD=2∠EDC.
解:(1)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠BAD=∠CAD,
∵∠BAD=30°,
∴∠BAD=∠CAD=30°,
∵AD=AE,
∴∠ADE=∠AED=75°,
∴∠EDC=15°.
(2)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠BAD=∠CAD,
∵∠BAD=40°,
∴∠BAD=∠CAD=40°,
∵AD=AE,
∴∠ADE=∠AED=70°,
∴∠EDC=20°.
(3)∠BAD=2∠EDC(或∠EDC=![]() ∠BAD)
∠BAD)
(4)仍成立,理由如下
∵AD=AE,∴∠ADE=∠AED,
∴∠BAD+∠B=∠ADC=∠ADE+∠EDC=∠AED+∠EDC=(∠EDC+∠C)+∠EDC
=2∠EDC+∠C
又∵AB=AC,
∴∠B=∠C
∴∠BAD=2∠EDC.
故分别填15°,20°,∠EDC=![]() ∠BAD
∠BAD