Question

【题目】如图，正方形ABCD的对角线AC，BD相交于点O，延长CB至点F，使CF=CA，连接AF，∠ACF的平分线分别交AF，AB，BD于点E，N，M，连接EO．

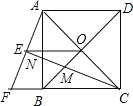
（1）已知BD=，求正方形ABCD的边长；

（2）猜想线段EM与CN的数量关系并加以证明．

Answer 1

【答案】（1）1；（2）CN=CM，理由详见解析.

【解析】

试题分析：（1）根据正方形的性质可得△ABD是等腰直角三角形，再由勾股定理可得2AB2=BD2，即可求得AB=1；（2）根据等腰三角形的性质可得CE⊥AF，再证得∠BAF=∠BCN，利用AAS证得△ABF≌△CBN，根据全等三角形的性质可得AF=CN，再证△ABF∽△COM，根据相似三角形的性质和正方形的性质即可证得CN=CM．

试题解析：（1）∵四边形ABCD是正方形，

∴△ABD是等腰直角三角形，

∴2AB2=BD2，

∵BD=，

∴AB=1，

∴正方形ABCD的边长为1；

（2）CN=CM．

证明：∵CF=CA，AF是∠ACF的平分线，

∴CE⊥AF，

∴∠AEN=∠CBN=90°，

∵∠ANE=∠CNB，

∴∠BAF=∠BCN，

在△ABF和△CBN中，

，

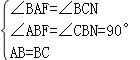∴△ABF≌△CBN（AAS），

∴AF=CN，

∵∠BAF=∠BCN，∠ACN=∠BCN，

∴∠BAF=∠OCM，

∵四边形ABCD是正方形，

∴AC⊥BD，

∴∠ABF=∠COM=90°，

∴△ABF∽△COM，

∴=，

∴==，

即CN=CM．