题目内容
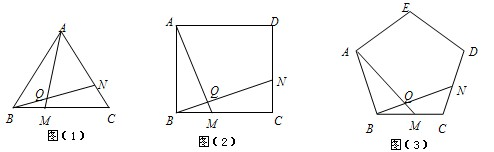
24、(1)如图(1),△ABC为正三角形,点M是BC上任一点,点N是边AC上任一点,且BM=CN,直线AM与BN相交于点Q.∠BQM等于多少度?请说明理由;
(2)如图(2),四边形ABCD为正方形,点M是BC上任一点,点N是边CD上任一点,且BM=CN,直线AM与BN相交于点Q.∠BQM等于多少度?简要说明理由;
(3)如图(3),在正五边形ABCDE中,点M是BC上任一点,点N是边CD上任一点,且BM=CN,直线AM与BN相交于点Q.∠BQM等于多少度?
(2)如图(2),四边形ABCD为正方形,点M是BC上任一点,点N是边CD上任一点,且BM=CN,直线AM与BN相交于点Q.∠BQM等于多少度?简要说明理由;
(3)如图(3),在正五边形ABCDE中,点M是BC上任一点,点N是边CD上任一点,且BM=CN,直线AM与BN相交于点Q.∠BQM等于多少度?

分析:本题是变式拓展题,需要从图(1)中寻找解题方法,图(2)(3)类似;从图(1)中不难得出△ABM≌△BCN,利用对应角相等,外角和定理可求∠BQM=60度.
解答:解:(1)∠BQM=60度.
理由:由条件得△ABM≌△BCN.
∴∠BAM=∠CBN.
∴∠BQM=∠BAQ+∠ABQ=∠CBN+∠ABN=∠ABC=60°.
(2)∠BQM=90°.理由同(1).
(3)∠BQM=108°.
理由:由条件得△ABM≌△BCN.
∴∠BAM=∠CBN.
∴∠BQM=∠BAQ+∠ABQ=∠CBN+∠ABN=∠ABC=60°.
(2)∠BQM=90°.理由同(1).
(3)∠BQM=108°.
点评:本题综合考查全等三角形、等边三角形和四边形的有关知识.注意对三角形全等性质的运用及学会对问题的拓展.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
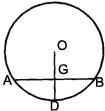 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=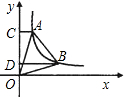 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

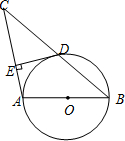 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.