题目内容
【题目】如图,△ABC中,A1,A2,A3,…,An为AC边上不同的n个点,首先连接BA1,图中出现了3个不同的三角形,再连接BA2,图中便有6个不同的三角形,……
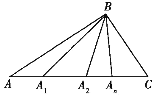
(1)完成下表:
连接个数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现三角形个数 | 3 | 6 |
(2)若出现了45个三角形,则共连接了_____个点?若一直连接到An,则图中共有______个三角形.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)8,
;(2)8,![]() .
.
【解析】
(1)根据图形,可以数三角形的个数,其实就是数AC上线段的个数,当1个分点时,有三角形数为![]() ,当2个分点时,有三角形数为
,当2个分点时,有三角形数为![]() ,由此可找出规律,据此即可得答案;
,由此可找出规律,据此即可得答案;
(2)由(1)继续推导可解得若出现了45个三角形,若一直连接到An,由![]() 个分点,三角形数量为前一个分点数的三角形总数加
个分点,三角形数量为前一个分点数的三角形总数加![]() 个,可知
个,可知![]() 个分点,则有
个分点,则有![]() 个三角形.
个三角形.
(1)由图形可得:数三角形的个数,其实就是数AC上线段的个数.
所以当1个分点时,有三角形数为![]() ;
;
2个分点时,有三角形数为![]() ;
;
3个分点时,有![]() ;
;
4个分点时,有![]() ;
;
5个分点时,有![]() ;
;
6个分点时,有![]() ;
;
(2)若出现45=1+2+3+4+5+6+7+8+9个三角形,根据上述规律,则有8个分点;
若有![]() 个分点,则有
个分点,则有![]() .
.

练习册系列答案
相关题目