题目内容
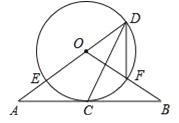
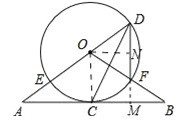
【题目】如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF、DC.已知OA=OB,CA=CB,DE=10,DF=6.
(1)求证:①直线AB是⊙O的切线;②∠FDC=∠EDC;
(2)求CD的长.
【答案】(1)①证明见解析;②证明见解析;(2)![]() .
.
【解析】
试题分析:(1)①欲证明直线AB是⊙O的切线,只要证明OC⊥AB即可.
②首先证明OC∥DF,再证明∠FDC=∠OCD,∠EDC=∠OCD即可.
(2)作ON⊥DF于N,延长DF交AB于M,在RT△CDM中,求出DM、CM即可解决问题.
试题解析:(1)①证明:连接OC.
∵OA=OB,AC=CB,∴OC⊥AB,∵点C在⊙O上,∴AB是⊙O切线.
②证明:∵OA=OB,AC=CB,∴∠AOC=∠BOC,∵OD=OF,∴∠ODF=∠OFD,∵∠AOB=∠ODF+∠OFD=∠AOC+∠BOC,∴∠BOC=∠OFD,∴OC∥DF,∴∠CDF=∠OCD,∵OD=OC,∴∠ODC=∠OCD,∴∠ADC=∠CDF.
(2)作ON⊥DF于N,延长DF交AB于M.
∵ON⊥DF,∴DN=NF=3,在RT△ODN中,∵∠OND=90°,OD=5,DN=3,∴ON=![]() =4,∵∠OCM+∠CMN=180°,∠OCM=90°,∴∠OCM=∠CMN=∠MNO=90°,∴四边形OCMN是矩形,∴ON=CM=4,MN=OC=5,在RT△CDM中,∵∠DMC=90°,CM=4,DM=DN+MN=8,∴CD=
=4,∵∠OCM+∠CMN=180°,∠OCM=90°,∴∠OCM=∠CMN=∠MNO=90°,∴四边形OCMN是矩形,∴ON=CM=4,MN=OC=5,在RT△CDM中,∵∠DMC=90°,CM=4,DM=DN+MN=8,∴CD=![]() =
=![]() =
=![]() .
.

练习册系列答案
相关题目