题目内容
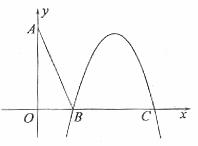
在直角坐标系xOy中,设点A(0,t),点Q(t,b)。平移二次函数![]() 的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(OB<OC),连结A,B。
的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(OB<OC),连结A,B。
(1)是否存在这样的抛物线F,使得![]() ?请你做出判断,并说明理由;
?请你做出判断,并说明理由;
(2)如果AQ∥BC,且tan∠ABO=![]() ,求抛物线F对应的二次函数的解析式。
,求抛物线F对应的二次函数的解析式。
解:(1)∵ 平移![]() 的图象得到的抛物线
的图象得到的抛物线![]() 的顶点为
的顶点为![]() ,
,
∴ 抛物线![]() 对应的解析式为:
对应的解析式为:![]() .
.
∵ 抛物线与x轴有两个交点,∴![]() .
.
令![]() , 得
, 得![]()
![]() ,
,![]()
![]() ,
,
∴ ![]()
![]() )(
)( ![]()
![]() )|
)| ![]()
即![]() , 所以当
, 所以当![]() 时, 存在抛物线
时, 存在抛物线![]() 使得
使得![]() .
.
(2) ∵![]() , ∴
, ∴ ![]() , 得
, 得![]() :
: ![]() ,
,
解得![]() .
.
在![]()
![]() 中,
中,
1) 当![]() 时,由
时,由 ![]() , 得
, 得![]() ,
,
当![]() 时, 由
时, 由![]()
![]()
![]()
![]()
![]()
![]() , 解得
, 解得![]() ,
,
此时, 二次函数解析式为![]() ;
;
当![]() 时, 由
时, 由![]()
![]()
![]()
![]()
![]()
![]() , 解得
, 解得![]()
![]() ,
,
此时,二次函数解析式为![]()
![]()
![]() +
+![]()
![]() +
+![]() .
.
2) 当![]() 时, 由
时, 由 ![]() , 将
, 将![]() 代
代![]() , 可得
, 可得![]()
![]() ,
, ![]() ,
,
(也可由![]() 代
代![]() ,
,![]() 代
代![]() 得到)
得到)
所以二次函数解析式为 ![]()
![]()
![]() +
+![]()
![]()
![]() 或
或![]() .
.

练习册系列答案
相关题目

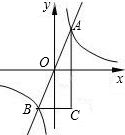 在直角坐标系xoy中,函数y=4x的图象与反比例函数y=
在直角坐标系xoy中,函数y=4x的图象与反比例函数y= (2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10).
(2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10). 析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.
析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.