题目内容
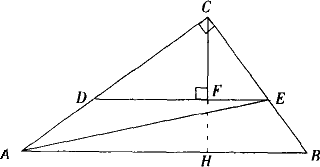
如下图,已知△ABC中,∠C=90°,AC=4,BC=3,DE∥AB,交AC于D,交BC于E,CF⊥DE于F,DE在△ABC内作平行运动,问DE为何值时,△ADE的面积最大,并求出这个最大值.
答案:
解析:
解析:
简解:延长CF交AB于H.
易求得AB=5,CH=![]() .
.
设FH=x,则CF=![]() -x.
-x.
∵DE∥AB.
∴![]() =
=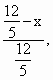
∴DE=5-![]() x.
x.
又设△ADE的面积为y,于是
y=![]() DE·FH=
DE·FH=![]() (5-
(5-![]() x)·x
x)·x
=-![]() x2+
x2+![]() x
x
=-![]() (x-
(x-![]() )2+
)2+![]() (0<x<
(0<x<![]() ).
).
∴当x=![]() ,即DE=
,即DE=![]() 时,△ADE的面积最大,最大值为
时,△ADE的面积最大,最大值为![]() .
.
分析:DE作为△ADE的底,延长CF交AB于H,可得到△ADE的高FH,通过设未知数建立等式向函数转化.
简评:几何问题向函数转化,函数的最大值发挥了决定的作用.
综上,解决几何最值问题,可直接考虑应用几何中的公里、定理,如线段最短公里、垂线段最短、角的不等关系等;或考虑取线段、点的极端位置,然后通过计算求最值;或把几何问题代数比,向方程、不等式、函数转化,用代数法求最值.解题时要根据题目特点具体分析,灵活掌握.

练习册系列答案
相关题目
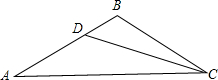 如下图,已知△ABC中,∠A=∠ACB,CD是∠ACB的平分线,∠ADC=150°,则∠ABC的度数为
如下图,已知△ABC中,∠A=∠ACB,CD是∠ACB的平分线,∠ADC=150°,则∠ABC的度数为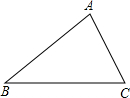 如下图,已知△ABC,在△ABC内部找一点P,使点P到AB、BC的距离相等,且点P到B、C两点的距离也相等.(写出作法并画出作图痕迹)
如下图,已知△ABC,在△ABC内部找一点P,使点P到AB、BC的距离相等,且点P到B、C两点的距离也相等.(写出作法并画出作图痕迹) 24、如下图,已知△ABC内接于⊙O,若∠C=45°,AB=4,求⊙O的面积.
24、如下图,已知△ABC内接于⊙O,若∠C=45°,AB=4,求⊙O的面积. 如下图,已知△ABC内接于⊙O,若∠C=45°,AB=4,求⊙O的面积.
如下图,已知△ABC内接于⊙O,若∠C=45°,AB=4,求⊙O的面积. 如下图,已知△ABC,在△ABC内部找一点P,使点P到AB、BC的距离相等,且点P到B、C两点的距离也相等.(写出作法并画出作图痕迹)
如下图,已知△ABC,在△ABC内部找一点P,使点P到AB、BC的距离相等,且点P到B、C两点的距离也相等.(写出作法并画出作图痕迹)