题目内容
24、如下图，已知△ABC内接于⊙O，若∠C=45°，AB=4，求⊙O的面积．分析：欲求⊙O的面积，关键是求出⊙O的半径；连接OA、OB，根据圆周角定理，易得∠AOB=90°，则△OAB是等腰直角三角形，由此可求出半径OA、OB的长，即可根据圆的面积公式求出⊙O的面积．
解答：
解：连接OA，OB；
则OA=OB，∠AOB=2∠C；（2分）
∵∠C=45°，∴∠AOB=90°，
∴OA2+OB2=AB2；（4分）
又∵AB=4，
∴2OA2=42，OA2=8；（6分）
∴S⊙O=π•OA2=8π．（8分）
解：连接OA，OB；则OA=OB，∠AOB=2∠C；（2分）
∵∠C=45°，∴∠AOB=90°，
∴OA2+OB2=AB2；（4分）
又∵AB=4，
∴2OA2=42，OA2=8；（6分）
∴S⊙O=π•OA2=8π．（8分）
点评：此题考查的是勾股定理以及圆周角定理的应用．能够由圆周角定理正确的判断出△OAB的形状是解答此题的关键．
练习册系列答案
相关题目
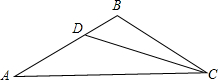如下图，已知△ABC中，∠A=∠ACB，CD是∠ACB的平分线，∠ADC=150°，则∠ABC的度数为
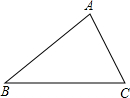如下图，已知△ABC，在△ABC内部找一点P，使点P到AB、BC的距离相等，且点P到B、C两点的距离也相等．（写出作法并画出作图痕迹）
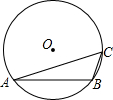如下图，已知△ABC内接于⊙O，若∠C=45°，AB=4，求⊙O的面积．
如下图，已知△ABC，在△ABC内部找一点P，使点P到AB、BC的距离相等，且点P到B、C两点的距离也相等．（写出作法并画出作图痕迹）