题目内容
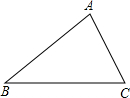 如下图,已知△ABC,在△ABC内部找一点P,使点P到AB、BC的距离相等,且点P到B、C两点的距离也相等.(写出作法并画出作图痕迹)
如下图,已知△ABC,在△ABC内部找一点P,使点P到AB、BC的距离相等,且点P到B、C两点的距离也相等.(写出作法并画出作图痕迹)已知:△ABC.
求作:一点P,使点P到AB、BC两边的距离相等,点P到B、C两点的距离也相等.
作法:
分析:由题意可知,P点不但要在∠B的角平分线上,而且也要在BC的中垂线上,故P点为∠B的角平分线和BC的中垂线的交点.
解答: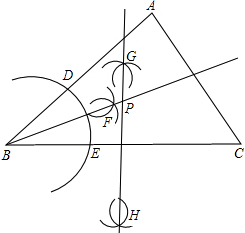 作法:(1)以B为圆心画弧交AB、BC于D、E两点,
作法:(1)以B为圆心画弧交AB、BC于D、E两点,
(2)分别以D、E两点为圆心,大于
DE长为半径画弧,两弧相交于F点,
(3)作射线BF,
(4)分别以B、C两点为圆心,大于
BC长为半径画弧,两弧分别相交于G、H两点,连接GH,
(5)BF与GH的交点就是所要求作的P点.
 作法:(1)以B为圆心画弧交AB、BC于D、E两点,
作法:(1)以B为圆心画弧交AB、BC于D、E两点,(2)分别以D、E两点为圆心,大于
| 1 |
| 2 |
(3)作射线BF,
(4)分别以B、C两点为圆心,大于
| 1 |
| 2 |
(5)BF与GH的交点就是所要求作的P点.
点评:本题主要考查线段中垂线上的点的性质、角平分线上点的性质、关键在于分析出P点为∠B的角平分线和BC的中垂线的交点,认真正确的画出作图痕迹.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
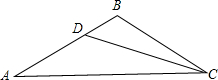 如下图,已知△ABC中,∠A=∠ACB,CD是∠ACB的平分线,∠ADC=150°,则∠ABC的度数为
如下图,已知△ABC中,∠A=∠ACB,CD是∠ACB的平分线,∠ADC=150°,则∠ABC的度数为 24、如下图,已知△ABC内接于⊙O,若∠C=45°,AB=4,求⊙O的面积.
24、如下图,已知△ABC内接于⊙O,若∠C=45°,AB=4,求⊙O的面积. 如下图,已知△ABC内接于⊙O,若∠C=45°,AB=4,求⊙O的面积.
如下图,已知△ABC内接于⊙O,若∠C=45°,AB=4,求⊙O的面积. 如下图,已知△ABC,在△ABC内部找一点P,使点P到AB、BC的距离相等,且点P到B、C两点的距离也相等.(写出作法并画出作图痕迹)
如下图,已知△ABC,在△ABC内部找一点P,使点P到AB、BC的距离相等,且点P到B、C两点的距离也相等.(写出作法并画出作图痕迹)