题目内容
已知在△ABC中,AB=2| 3 |
| 3 |
(1)求BC的长;
(2)若有一个正方形的一边在AB上,另外两个顶点分别在AC和BC上,求正方形的面积.
分析:(1)根据题中所给的条件,应分两种情况进行讨论,AD在△ABC内部和外部;
(2)设正方形边长为x,根据平行线比例关系,解得正方形边长,从而求出正方形的面积.
(2)设正方形边长为x,根据平行线比例关系,解得正方形边长,从而求出正方形的面积.
解答:解:根据条件显然有两种情况,如图,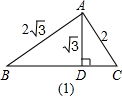
(1)在图(1)中,可求CD=1,∠CAD=30°,
∴∠B=30°,∠C=60°,
∴△ABC是直角三角形,
∴BC=4.
在图(2)中,可求CD=1,∠CAD=30°,∠B=30°,
∴∠BAD=60°,△ABC是等腰三角形,AC平分∠BAD,
BC=AC=2.
(2)在图(3)中,设正方形边长为x,
∵
=
,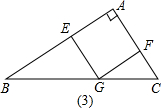
∴
=
,
解得x=3-
,
∴S正方形=12-6
(当BC=4时),
在图(4)中,当BC=2时,
∵AC=2,
∴△ABC是等腰三角形,此时内接正方形h是△ABC的AB边上的高,
h=
=1,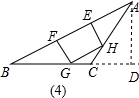
设正方形边长为x,由△HGC∽△ABC得,
=
,即
=
,
解得x=
,
∴S正方形=
(当BC=2时).

(1)在图(1)中,可求CD=1,∠CAD=30°,
∴∠B=30°,∠C=60°,
∴△ABC是直角三角形,
∴BC=4.
在图(2)中,可求CD=1,∠CAD=30°,∠B=30°,

∴∠BAD=60°,△ABC是等腰三角形,AC平分∠BAD,
BC=AC=2.
(2)在图(3)中,设正方形边长为x,
∵
| EG |
| AC |
| BE |
| AB |

∴
| x |
| 2 |
2
| ||
2
|
解得x=3-
| 3 |
∴S正方形=12-6
| 3 |
在图(4)中,当BC=2时,
∵AC=2,
∴△ABC是等腰三角形,此时内接正方形h是△ABC的AB边上的高,
h=
22-(
|

设正方形边长为x,由△HGC∽△ABC得,
| HG |
| AB |
| hx |
| h |
| x | ||
2
|
| 1-x |
| 1 |
解得x=
2
| ||
2
|
∴S正方形=
156-48
| ||
| 121 |
点评:本题在求解时应分情况进行讨论,还考查解直角三角形的定义及正方形面积公式,由直角三角形已知元素求未知元素的过程,只要理解直角三角形中边角之间的关系即可求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.
22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数. 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC.
如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC. 如图,已知在△ABC中,∠B与∠C的平分线交于点P.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.