题目内容
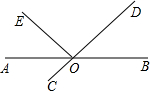
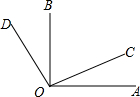
如图,点A、O、C在一直线上,OE是∠BOC的平分线,∠EOF=90°,∠1=(4x+20)°,∠2=(x-10)°.
(1)求:∠1的度数;(请写出解题过程)
(2)如以OF为一边,在∠COF的外部画∠DOF=∠COF,问边OD与边OB成一直线吗?
请说明理由.

(1)求:∠1的度数;(请写出解题过程)
(2)如以OF为一边,在∠COF的外部画∠DOF=∠COF,问边OD与边OB成一直线吗?
请说明理由.

(1)因为OE是∠BOC的平分线所以∠BOC=2∠2,
因为点A、O、C在一直线上所以∠1+∠BOC=180°,
因为∠1=(4x+20)°,∠2=(x-10)°,
所以(4x+20)+2(x-10)=180,
解得:x=30,∠1=140°,
所以∠1的度数为140°;
(2)边OD与边OB成一直线,
因为∠EOF=∠EOC+∠COF=90°
又因为∠EOC=
∠BOC,∠FOC=
∠DOC,
∠BOC+
∠DOC=90°,
即∠BOC+∠DOC=180°,
所以点D、O、B在一直线上,
即边OD与边OB成一直线.
因为点A、O、C在一直线上所以∠1+∠BOC=180°,
因为∠1=(4x+20)°,∠2=(x-10)°,
所以(4x+20)+2(x-10)=180,
解得:x=30,∠1=140°,
所以∠1的度数为140°;
(2)边OD与边OB成一直线,
因为∠EOF=∠EOC+∠COF=90°
又因为∠EOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即∠BOC+∠DOC=180°,
所以点D、O、B在一直线上,
即边OD与边OB成一直线.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目