Question

填写证明的理由．
已知：如图，AB∥CD，EF、CG分别是∠AEC、∠ECD的角平分线；求证：EF∥CG．
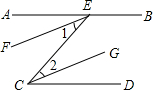
证明：∵AB∥CD（已知）
∴∠AEC=∠DCE      （

 

）
又∵EF平分∠AEC    （已知）
∴∠1=

1

2

∠AEC     （

 

）
同理∠2=

1

2

∠DCE，∴∠1=∠2
∴EF∥CG           （

 

）

Answer 1

分析：根据平行线的性质可填第一个空；根据角平分线的性质可填第二个空；根据平行线的判定可填第三个空．

解答：证明：∵AB∥CD（已知），
∴∠AEC=∠DCE （两直线平行，内错角相等）；
又∵EF平分∠AEC（已知），
∴∠1=

1

2

∠AEC（角平分线的定义），
同理∠2=

1

2

∠DCE，
∴∠1=∠2，
∴EF∥CG （内错角相等，两直线平行）．

点评：本题考查了平行线的判定及平行线的性质，涉及到角平分线的定义，比较简单．