题目内容
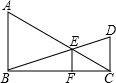如图，AB、CD分别垂直于直线BC，AC和BD相交于E，过点E作EF⊥BC于F．若AB=80，CD=20，那么EF等于（ ）| A、40 | B、25 | C、20 | D、16 |
分析：由AB⊥BC，CD⊥BC，EF⊥BC，即可得AB∥EF∥CD，然后根据平行线分线段成比例定理，即可求得
=
与
=
，又由AB=80，CD=20，即可求得
的值，继而求得答案．
| AB |
| CD |
| AE |
| CE |
| CE |
| AC |
| EF |
| AB |
| CE |
| AC |
解答：解：∵AB⊥BC，CD⊥BC，EF⊥BC，
∴AB∥EF∥CD，
∴
=
，
∵AB=80，CD=20，
∴
=
=4，
∴
=
，
∵
=
，
∴
=
，
∴EF=16．
故选D．
∴AB∥EF∥CD，
∴
| AB |
| CD |
| AE |
| CE |
∵AB=80，CD=20，
∴
| AE |
| CE |
| 80 |
| 20 |
∴
| CE |
| AC |
| 1 |
| 5 |
∵
| CE |
| AC |
| EF |
| AB |
∴
| EF |
| 80 |
| 1 |
| 5 |
∴EF=16．
故选D．
点评：此题考查了平行线分线段成比例定理．此题难度不大，解题的关键是注意数形结合思想的应用与比例变形．
练习册系列答案
相关题目
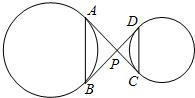如图，AB、CD分别为两圆的弦，AC、BD为两圆的公切线且相交于P点．若PC=2，CD=3，
（2013•丹东一模）如图，AB、CD分别表示甲、乙两建筑物的高，从A点测得D点的仰角为30°，从B点测得D点的仰角为60°，已知两楼之间的距离为27米．求甲、乙两建筑物的高AB、CD．（结果精确到个位）（参考数据：
如图，AB，CD分别与EF相交于点G，H，N是CD上一点，已知∠AGE=135°，∠HGN=65°，∠GNH=70°．试判断AB与CD是否平行，为什么？