Question

（2013•丹东一模）如图，AB、CD分别表示甲、乙两建筑物的高，从A点测得D点的仰角为30°，从B点测得D点的仰角为60°，已知两楼之间的距离为27米．求甲、乙两建筑物的高AB、CD．（结果精确到个位）（参考数据：

2

≈1.4，

3

≈1.7）

Answer 1

分析：先作AE⊥CD于点E，得出AE=BC-27，AB=CE，根据tan∠DBC=

CD

BC

，求出CD的长，再根据tan∠DAE=

DE

AE

，求出DE的长，最后根据CE=CD-DE，即可得出答案．

解答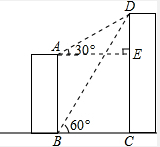：解：作AE⊥CD于点E，则四边形ABCE为矩形，
则AE=BC-27，AB=CE，
在Rt△BCD中，
∵tan∠DBC=

CD

BC

，
∴CD=

3

×27=27

3

≈46（米），
在Rt△AED中，
∵tan∠DAE=

DE

AE

，
∴DE=

3

3

×27=9

3

，
∴CE=CD-DE=27

3

-9

3

=18

3

，
∴AB=CE=18

3

≈31（米）；
答：甲、乙两建筑物的高AB、CD分别为31米和46米．

点评：此题考查了解直角三角形的应用-仰角俯角问题，本题要求学生借助俯角构造直角三角形，并结合图形利用三角函数解直角三角形．