题目内容
【题目】如图，A（6，0），B（0，4），点B关于x轴的对称点为C点，点D在x轴的负半轴上，△ABD的面积是30．
（1）求点D坐标；
（2）若动点P从点B出发，沿射线BC运动，速度为每秒1个单位，设P的运动时间为t秒，△APC的面积为S，求S与t的关系式；
（3）在（2）的条件下，同时点Q从D点出发沿x轴正方向以每秒2个单位速度匀速运动，若点R在过A点且平行于y轴的直线上，当△PQR为以PQ为直角边的等腰直角三角形时，求满足条件的t值．
【答案】（1）点D坐标为（﹣9，0）；（2）当0＜t≤8时，S＝﹣3t+24，当t＞8时，S＝3t﹣24．（3）当△PQR为以PQ为直角边的等腰直角三角形时，t＝6秒或
秒或10秒或11秒．
【解析】
（1）根据三角形面积公式求出AD即可．
（2）分两种情形①当0＜t≤8时，②当t＞8时，求出△PAC面积即可．
（3）分三种情形①如图1中，当∠QPR=90°，PQ=PR时，作RH⊥OP于H，②如图2中，当∠PQR=90°，QR=PQ时，③如图3中，当∠PQR＝90°，QR＝PQ时利用全等三角形的性质列出方程即可解决．
（1）∵A（6，0），B（0，4），△ABD的面积是30，
∴
，
∴
，
∴AD＝15，
∴OD＝9，
∴点D坐标为（﹣9，0）；
（2）∵点B（0，4）关于x轴的对称点为C点，
∴点C坐标（0﹣4），
∴当0＜t≤8时，S＝
×（8﹣t）×6＝﹣3t+24，
当t＞8时，S＝ ×（t﹣8）×6＝3t﹣24．
（3）①如图1中，当∠QPR＝90°，PQ＝PR时，作RH⊥OP于H，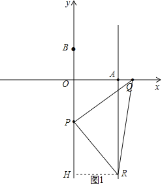
∵∠QPO+∠RPH＝90°，∠QPO+∠PQO＝90°，
∴∠PQO＝∠RPH，
在△PQO和△RPH中，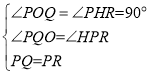
，
∴△PQO≌△RPH（AAS），
∴RH＝PO，
∵四边形AOHR是矩形，
∴RH＝AO＝6，
∴OP＝6，
∴t﹣4＝6，
∴t＝10；
②如图2中，当∠PQR＝90°，QR＝PQ时，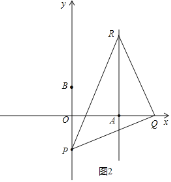
∵∠RQA+∠OQP＝90°，∠OQP+∠OPQ＝90°，
∴∠RQA＝∠OPQ，
在△ARQ和△OQP中，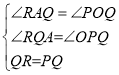
，
∴△ARQ≌△OQP，
∴OP＝AQ，
∴t﹣4＝2t﹣15，
∴t＝11；
③如图3中，当∠PQR＝90°，QR＝PQ时，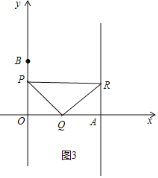
∵∠RQA+∠OQP＝90°，∠OQP+∠OPQ＝90°，
∴∠RQA＝∠OPQ，
在△ARQ和△OQP中，，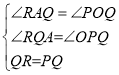
∴△ARQ≌△OQP，
∴OP＝AQ，
∴t﹣4＝15﹣2t，
∴
，
当Q为OA的中点，即2t﹣9＝3时，
∴t＝6；
综上所述，当△PQR为以PQ为直角边的等腰直角三角形时，t＝6秒或秒或10秒或11秒．
