题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
解:a、c同号(或当a>0时,c>0,当a<0时,c<0). |
(2) |
证明:设点A的坐标为(x1,0),点B的坐标为(x2,0),则0<x1<x2.∴OA=x1,OB=x2,OC=|c|,据题意,x1,x2是方程a x2+bx+c=0(a≠0)的两个根,∴x1·x2= |
(3) |
解:当b=-4时,由(2)知,x1+x2=- 解法一:AB=OB-OA=x2-x1= 解法二:由求根公式, |

练习册系列答案
相关题目
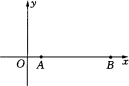
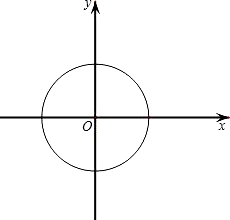 已知在平面直角坐标系xOy中,⊙O的半径为1.
已知在平面直角坐标系xOy中,⊙O的半径为1.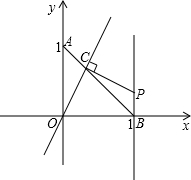 直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y),
直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y), 如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.
如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.