题目内容
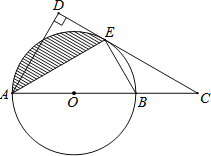
【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.
(1)求证:△ODM∽△MCN;
(2)设DM=x,OA=R,求R关于x的函数关系式;
(3)在动点O逐渐向点D运动(OA逐渐增大)的过程中,△CMN的周长如何变化?说明理由.

【答案】(1)存在△MCN与△ODM相似,证明见矩形;
(2)R=![]() ;
;
(3)△CMN的周长是一个定值,理由见解析.
【解析】试题分析:(1)根据切线的性质得出∠OMN=90,从而证得∠OMD=∠MNC;则△ODM∽△MCN;
(2)由DM=x,设OA=OM=R;则得出OD,由勾股定理得R与x的关系;
(3)可分为两种解法得出答案.由△ODM∽△MCN,得![]() ,用含x的式子表示出CN,MN,从而得出△CMN的周长是一个定值.
,用含x的式子表示出CN,MN,从而得出△CMN的周长是一个定值.
试题解析:(1)存在△MCN与△ODM相似,证明如下:
∵MN切⊙O于点M,∴∠OMN=90°,∵∠OMD+∠CMN=90°,∠CMN+∠CNM=90°,∴∠OMD=∠MNC,又∵∠D=∠C=90°,∴△ODM∽△MCN.
(2)在Rt△ODM中,DM=x,设OA=OM=R,∴OD=AD﹣OA=8﹣R,由勾股定理得:(8﹣R)2+x2=R2,
∴64﹣16R+R2+x2=R2,∴R=![]() .
.
(3)∵CM=CD﹣DM=8﹣x,OD=8﹣R=8﹣![]() ,且有△ODM∽△MCN,∴
,且有△ODM∽△MCN,∴![]() ,∴代入得到:CN=
,∴代入得到:CN=![]() .
.
同理![]() ,∴代入得到:MN=
,∴代入得到:MN=![]() ,∴△CMN的周长=CM+CN+MN=(8﹣x)+
,∴△CMN的周长=CM+CN+MN=(8﹣x)+![]() +
+![]() =(8﹣x)+(x+8)=16,
=(8﹣x)+(x+8)=16,
在点O的运动过程中,△CMN的周长始终为16,是一个定值.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案
相关题目