题目内容
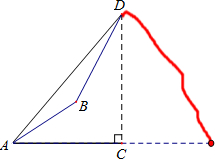 如图,由山脚下的一点A测得山顶D的仰角是45°,从A沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,则山高CD为( )
如图,由山脚下的一点A测得山顶D的仰角是45°,从A沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,则山高CD为( )分析:首先根据题意分析图形;过点B作CD,AC的垂线,垂足分别为E,F,构造两个直角三角形△ABF与△BDE,分别求解可得DF与EB的值,再利用图形关系,进而可求出答案.
解答: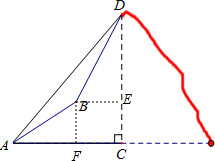 解:过点B作CD,AC的垂线,垂足分别为E,F,
解:过点B作CD,AC的垂线,垂足分别为E,F,
∵∠BAC=30°,AB=1500米,
∴BF=EC=750米.
AF=AB•cos∠BAC=1500×
=750
米.
设FC=x米,
∵∠DBE=60°,
∴DE=
x米.
又∵∠DAC=45°,
∴AC=CD.
即:750
+x=750+
x,
解得x=750.
则CD=750(
+1)米.
故选C.
 解:过点B作CD,AC的垂线,垂足分别为E,F,
解:过点B作CD,AC的垂线,垂足分别为E,F,∵∠BAC=30°,AB=1500米,
∴BF=EC=750米.
AF=AB•cos∠BAC=1500×
| ||
| 2 |
| 3 |
设FC=x米,
∵∠DBE=60°,
∴DE=
| 3 |
又∵∠DAC=45°,
∴AC=CD.
即:750
| 3 |
| 3 |
解得x=750.
则CD=750(
| 3 |
故选C.
点评:本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
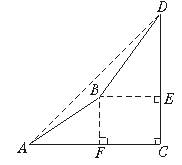
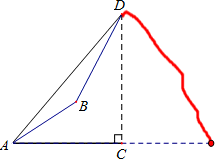 如图,由山脚下的一点A测得山顶D的仰角是45°,从A沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,则山高CD为
如图,由山脚下的一点A测得山顶D的仰角是45°,从A沿倾斜角为30°的山坡前进1500米到B,再次测得山顶D的仰角为60°,则山高CD为 +1)米
+1)米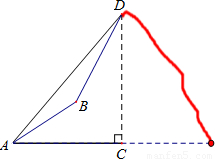
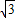 +1)米
+1)米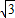 +1)米
+1)米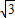 +1)米
+1)米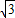 +1)米
+1)米