��Ŀ����
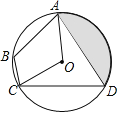
����Ŀ����ͼ1����֪![]() �У�
��![]() ��
��![]() ��
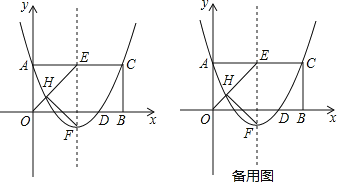
��![]() ������ƽ��ֱ������ϵ��λ����ͼ��ʾ����
������ƽ��ֱ������ϵ��λ����ͼ��ʾ����![]() ��
��![]() ��ĸ������ϣ���
��ĸ������ϣ���![]() �ڵ�
�ڵ�![]() ���Ҳࣩ������
���Ҳࣩ������![]() �ڵڶ����ޣ���
�ڵڶ����ޣ���![]() ��
��![]() ���ڵ�ֱ�߷��ۣ���
���ڵ�ֱ�߷��ۣ���![]() ���ڵ�
���ڵ�![]() λ��
�
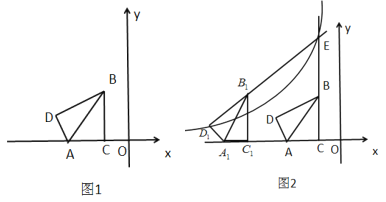
��1������![]() ����Ϊ
����Ϊ![]() ʱ�����
ʱ�����![]() �����ꣻ
�����ꣻ
��2������![]() �͵�
�͵�![]() ��ͬһ��������������ͼ���ϣ����
��ͬһ��������������ͼ���ϣ����![]() ���ꣻ
���ꣻ
��3����ͼ2�����ı���![]() ����ƽ�ƣ�ƽ�ƺ���ı��μ����ı���
����ƽ�ƣ�ƽ�ƺ���ı��μ����ı���![]() ������
������![]() �ķ���������
�ķ���������![]() ��ͼ����
��ͼ����![]() ���ӳ��߽��ڵ�
���ӳ��߽��ڵ�![]() ������ƽ�ƹ����У��Ƿ����������
������ƽ�ƹ����У��Ƿ����������![]() ��ʹ���Ե�
��ʹ���Ե�![]() Ϊ�������������ֱ���������ҵ�
Ϊ�������������ֱ���������ҵ�![]() ��ͬһ��ֱ���ϣ������ڣ����
��ͬһ��ֱ���ϣ������ڣ����![]() ��ֵ���������ڣ���˵������
��ֵ���������ڣ���˵������
���𰸡���1��![]() ����2��
����2��![]() ����3�����ڣ�
����3�����ڣ�![]() ��
��![]()
��������
��1������![]() ��
��![]() ���ڵ�
���ڵ�![]() ���������Ǻ���ֵ�ɵó�
���������Ǻ���ֵ�ɵó�![]() ���ٸ��ݷ��۵����ʿɵó�
���ٸ��ݷ��۵����ʿɵó�![]() ��
��![]() ���ٽ�
���ٽ�![]() ���ó�
���ó�![]() ��
��![]() ������ϵ�C�����꼴�ɵó��𰸣�
������ϵ�C�����꼴�ɵó��𰸣�
��2�����![]() ����Ϊ
����Ϊ![]() ��
��![]() �������
�������![]() ��������
��������![]() �����ã�1���ó��Ľ����Ϊ��֪�������ɵó���D������Ϊ
�����ã�1���ó��Ľ����Ϊ��֪�������ɵó���D������Ϊ![]() ���ٽ�Ϸ�����������⼴�ɣ�
���ٽ�Ϸ�����������⼴�ɣ�
��3�����ȴ���������kֵ����![]() ��
��![]() ����������۷������ɣ�
����������۷������ɣ�
�⣺��1����ͼ������![]() ��
��![]() ���ڵ�
���ڵ�![]()
��![]() ��
��
��![]()
��![]()
�������֪![]() ��
��![]() .
.
��![]() .
.
��![]()
��![]() ��
��![]() ��
��
��![]() ��
��![]() .
.
�ߵ�![]() ����Ϊ
����Ϊ![]() ��
��
��![]() .
.
���![]() ��������
��������![]()
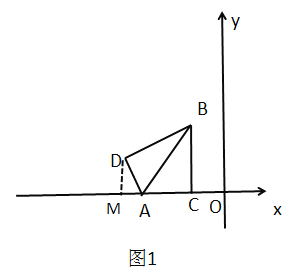
��2�����![]() ����Ϊ
����Ϊ![]() ��
��![]() �������
�������![]() ��������
��������![]() ��
��
�ɣ�1����֪����![]() ��������
��������![]()
�ߵ�![]() �͵�
�͵�![]() ��ͬһ��������������ͼ���ϣ�
��ͬһ��������������ͼ���ϣ�
��![]() .���
.���![]() .
.
���![]() ����Ϊ
����Ϊ![]()
��3������������![]() ��ʹ���Ե�
��ʹ���Ե�![]() ��
��![]() ��
��![]() Ϊ�������������ֱ��������
Ϊ�������������ֱ��������
�⣺�ٵ�![]() ʱ.
ʱ.
��ͼ��ʾ������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() .
.
��![]() ��
��![]() ��
��![]() .
.
��![]() ��
��![]()
��![]()
��![]()
�֡�![]() ��
��
��![]() ��
��![]() .
.
��![]() ��
��![]() ��
��
��![]() .
.
��![]() ��
��![]()
��![]() ��
��![]() ������
������![]() ��
��
��![]() ��
��![]() ��ͬһ����������ͼ���ϣ�
��ͬһ����������ͼ���ϣ�
��![]() .��ã�
.��ã�![]() .
.
��![]()
��![]()
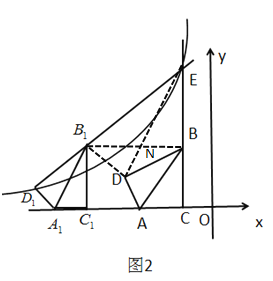
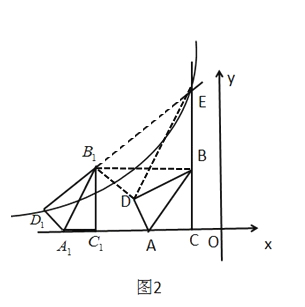
�ڵ�![]() ʱ.��ͼ��ʾ������
ʱ.��ͼ��ʾ������![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() .
.
��![]() ��
�У�
��![]() ��
��![]() ��
��
��![]() .
.
��![]() ��
�У�
��![]() ��
��
��![]() .
.
��![]()
��![]() ��
��![]() ������
������![]()
��![]() ��
��![]() ��ͬһ����������ͼ���ϣ�
��ͬһ����������ͼ���ϣ�
��![]() .
.
��ã�![]() ��
��
��![]()
��![]()

 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�