题目内容
【题目】在![]() 中,
中,![]() ,
,![]() 为高,
为高,![]()
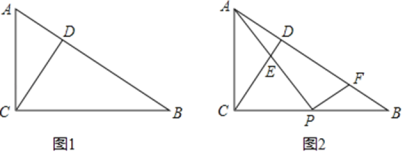
(1)如图1,当![]() 时,求
时,求![]() 的值;
的值;
(2)如图2,点![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 于
于![]() ,求
,求![]() 的值;(用含
的值;(用含![]() 的代数式表示)
的代数式表示)
(3)在(2)的条件下,若![]() ,则
,则![]() .(直接写出结果)
.(直接写出结果)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用已知条件可知△ADC∽△CDB,利用相似三角形的性质:对应边成比例即可解;
(2)要求![]() 的值,想办法把
的值,想办法把![]() 放在两个三角形中,只要两个三角形相似,找到相似比即可求,但根据图2没有发现这样的两个三角形,所以添加辅助线,过点P作PG∥AC,可得△PCE∽△PGF,进而利用相似三角形对应边成比例即可得出答案;
放在两个三角形中,只要两个三角形相似,找到相似比即可求,但根据图2没有发现这样的两个三角形,所以添加辅助线,过点P作PG∥AC,可得△PCE∽△PGF,进而利用相似三角形对应边成比例即可得出答案;
(3)由第二问中的结论,进而求出AF,AP的长,然后再Rt△APF中运用勾股定理即可.
解:(1)∵CD⊥AB
∴∠ADC=∠CDB=90°
∵∠A+∠ACD=90°,∠BCD+∠ACD=90°
∴∠A=∠BCD
![]() ∽
∽![]() ,
,
得![]() =
=![]() ,
,
![]()
![]()
(2)过点P作PG∥AC交AB于点G.
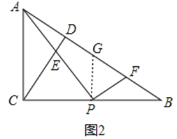
∴∠PGF=∠CAD,∠GPC=90°,
∵CD⊥AB,∠ACB=90°,
∴∠CAD+∠ACD=90°,∠ACD+∠PCE=90°,
∴∠PCE=∠CAD,
∴∠PCE=∠PGF,
又∵PF⊥AP,
∴∠CPE+∠APG=∠FPG+∠APG=90°,
∴∠CPE=∠GPF,
∴△PCE∽△PGF,
∴![]() ,
,
又∵点P是BC的中点,
∴AC=2PG,
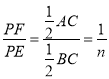
(3)由(2)设PF=x,PE=2x
∵PF=BF
∴∠FPB=∠FBP
∵∠GPB=90°
∴∠GPF+∠FPB=90°∠PGB+∠FBP=90°,
∴∠FGP=∠FPG
∴PF=BF=GF=x
∴AG=BG=2x
∴AF=AG+GF=3x
∵△PCE∽△PGF
∴![]()
∴CE=PE=nx
∵∠ACB=90°
∴∠ACE+∠
∵CE=PE=nx
∴∠ECP=∠EPC
∴∠ACE=∠CAP
∴CE=AE=PE
∴AE=PE=nx
∴AP=AE+PE=2nx
在Rt△APF中,
![]()
即![]()
∴![]()

【题目】已知一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 0 | p | m | 3 |
| q | 0 | … |
(1)求这个二次函数的表达式;
(2)表格中字母m= ;(直接写出答案)
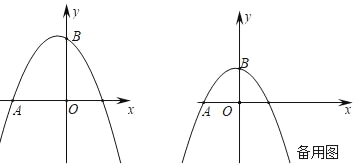
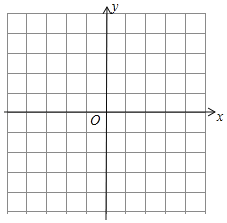
(3)在给定的直角坐标系中,画出这个二次函数的图象;
(4)以上二次函数的图象与x轴围成的封闭区域内(不包括边界),横、纵坐标都是整数的点共有 个.(直接写出结果)
【题目】已知:二次函数![]()
![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
| … |
| 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | m | … |
(1) 观察上表可求得![]() 的值为________;
的值为________;
(2) 试求出这个二次函数的解析式;
(3) 若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,请直接写出n的取值范围.