题目内容
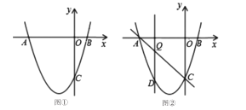
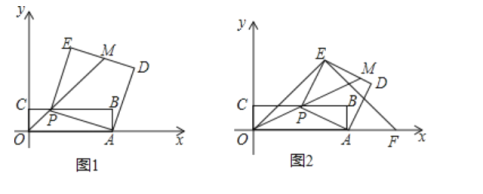
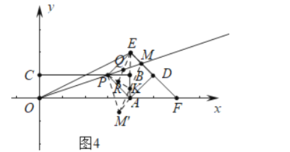
【题目】已知:如图1,矩形OABC的两个顶点A,C分别在x轴,y轴上,点B的坐标是(8,2),点P是边BC上的一个动点,连接AP,以AP为一边朝点B方向作正方形PADE,连接OP并延长与DE交于点M,设![]() .
.
(1)请用含a的代数式表示点P,E的坐标.
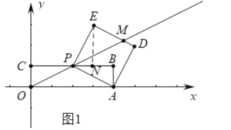
(2)如图2,连接OE,并把OE绕点E逆时针方向旋转90°得EF.若点F恰好落在x轴的正半轴上,求a与![]() 的值.
的值.
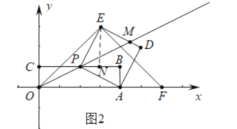
(3)如图1,若点M为DE的中点,并且![]() ,点
,点![]() 在OP的延长线上,求
在OP的延长线上,求![]() 的最小值.
的最小值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
, ![]() ;(3)
;(3)![]() .
.
【解析】
①根据一线三垂模型构造两个全等直角三角形,根据对应边相等,即可用a的代数式表示出E点坐标.
②根据旋转性质得出![]() 是等腰直角三角形,求出a的值和P,D,E三点坐标,再求出PO,DE两条直线交点,从而求出M点坐标,即可求出EM,DM的长度,求出比值.
是等腰直角三角形,求出a的值和P,D,E三点坐标,再求出PO,DE两条直线交点,从而求出M点坐标,即可求出EM,DM的长度,求出比值.
③构造相似,用a的代数式表示出M点坐标,再根据三角函数值相等列出等式方程和a的范围,求出a值,再通过旋转构造出等腰直角三角形,从而转化到求两条线段和的最小值,根据三点共线最短,进而求出两直线交点,利用两点间的距离公式即可求出具体值.
解:(1)如图1中,作![]() 于N.
于N.
∵![]() ,∴
,∴![]() ,
,![]() ,∵
,∵![]() ,∴
,∴![]()
∵四边形OABC是矩形,四边形ADEP是正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() .
.
(2)如图2中,由题意:![]() 是等腰直角三角形,∴
是等腰直角三角形,∴![]()
∵![]() ,∴
,∴![]()
∴![]() ,
,![]() ,
,![]() ,
,![]()
∴直线OP的解析式为![]() ,直线DE的解析式为
,直线DE的解析式为![]()
由![]()
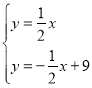 ,解得
,解得![]()
∴![]() ,∴
,∴![]() ,
,![]()
∴![]()
(3)如图3中,作![]() 于K.
于K.
由![]() ,可得,
,可得,![]()
∴![]() ,
,![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]()
∴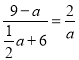 ,整理得:
,整理得:![]() ,解得
,解得![]() 或6
或6
∵![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
如图4中,将![]() 绕点P顺时针旋转90°得到
绕点P顺时针旋转90°得到![]() ,则
,则![]() 是等腰直角三角形.
是等腰直角三角形.
∴![]() 的中点
的中点![]()
∵![]() ,∴
,∴![]()
作![]() ,则
,则![]() ,∴
,∴![]()
∴当E、Q、R共线时,![]() 的值最小
的值最小
∵直线PR的解析式为![]() ,∵
,∵![]() ,∴直线ER的解析式为
,∴直线ER的解析式为![]()
由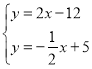 ,解得
,解得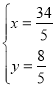 ,∴
,∴![]()
∴![]() ,∴
,∴![]() 的最小值为
的最小值为![]()

 特高级教师点拨系列答案
特高级教师点拨系列答案【题目】王老师从本校九年级质量检测的成绩中随机地抽取一些同学的数学成绩做质量分析,他先按照等级绘制这些人数学成绩的扇形统计图,如图(1)所示,数学成绩等级标准见表1,又按分数段绘制成绩分布表,如表2,
表1
等级 | 分数x的范围 |
A | a≤x≤100 |
B | 80≤x<a |
C | 60≤x<80 |
D | 0≤x<60 |
表2
分数段 | x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
人数 | 5 | 10 | m | 12 | n |
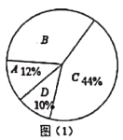
分数段为90≤x≤100的n个人中,其成绩的中位数是95分.
根据以上信息回答下面问题:
(1)王老师抽查了多少人?m、n的值分别是多少;
(2)小明在此考试中得了95分,他说自己在这些考试中数学成绩是A等级,他说的对吗?为什么?
(3)若此次测试数学学科普高的预测线是70分,该校九年级有900名学生,求数学学科达到普高预测线的学生约有多少人?
【题目】某校为了解学生课外阅读情况,就学生每周阅读时间随机调查了部分学生,调查结果按性别整理如下:
女生阅读时间人数统计表
阅读时间 | 人数 | 占女生人数百分比 |
| 4 |
|
|
|
|
| 5 |
|
| 6 |
|
| 2 |
|
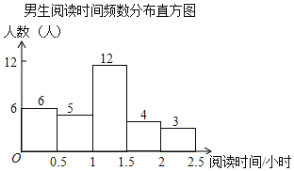
根据图表解答下列问题:
(1)在女生阅读时间人数统计表中,![]() ,
,![]() ;
;
(2)此次抽样调查中,共抽取了 名学生,学生阅读时间的中位数在 时间段;
(3)从阅读时间在2~2.5小时的5名学生中随机抽取2名学生参加市级阅读活动,恰好抽到男女生各一名的概率是多少?