题目内容
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于A(﹣1,0),B(5,0)两点.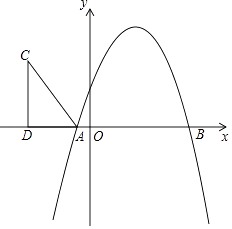
(1)求抛物线的解析式;
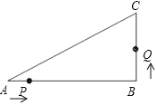
(2)在第二象限内取一点C,作CD垂直X轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵抛物线y=﹣x2+bx+c与x轴分别交于A(﹣1,0),B(5,0)两点,
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为y=﹣x2+4x+5;
(2)
解:∵AD=5,且OA=1,
∴OD=6,且CD=8,
∴C(﹣6,8),
设平移后的点C的对应点为C′,则C′点的纵坐标为8,
代入抛物线解析式可得8=﹣x2+4x+5,解得x=1或x=3,
∴C′点的坐标为(1,8)或(3,8),
∵C(﹣6,8),
∴当点C落在抛物线上时,向右平移了7或9个单位,
∴m的值为7或9;
(3)
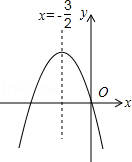
解:∵y=﹣x2+4x+5=﹣(x﹣2)2+9,
∴抛物线对称轴为x=2,
∴可设P(2,t),
由(2)可知E点坐标为(1,8),
①当BE为平行四边形的边时,连接BE交对称轴于点M,过E作EF⊥x轴于点F,当BE为平行四边形的边时,过Q作对称轴的垂线,垂足为N,如图,

则∠BEF=∠BMP=∠QPN,
在△PQN和△EFB中

∴△PQN≌△EFB(AAS),
∴NQ=BF=OB﹣OF=5﹣1=4,
设Q(x,y),则QN=|x﹣2|,
∴|x﹣2|=4,解得x=﹣2或x=6,
当x=﹣2或x=6时,代入抛物线解析式可求得y=﹣7,
∴Q点坐标为(﹣2,﹣7)或(6,﹣7);
②当BE为对角线时,
∵B(5,0),E(1,8),
∴线段BE的中点坐标为(3,4),则线段PQ的中点坐标为(3,4),
设Q(x,y),且P(2,t),
∴x+2=3×2,解得x=4,把x=4代入抛物线解析式可求得y=5,
∴Q(4,5);
综上可知Q点的坐标为(﹣2,﹣7)或(6,﹣7)或(4,5).
【解析】(1)由A、B的坐标,利用待定系数法可求得抛物线的解析式;(2)由题意可求得C点坐标,设平移后的点C的对应点为C′,则C′点的纵坐标为8,代入抛物线解析式可求得C′点的坐标,则可求得平移的单位,可求得m的值;(3)由(2)可求得E点坐标,连接BE交对称轴于点M,过E作EF⊥x轴于点F,当BE为平行四边形的边时,过Q作对称轴的垂线,垂足为N,则可证得△PQN≌△EFB,可求得QN,即可求得Q到对称轴的距离,则可求得Q点的横坐标,代入抛物线解析式可求得Q点坐标;当BE为对角线时,由B、E的坐标可求得线段BE的中点坐标,设Q(x,y),由P点的横坐标则可求得Q点的横坐标,代入抛物线解析式可求得Q点的坐标.
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.