题目内容
【题目】如图1,已知△ABC是等腰三角形,且∠ACB=90°,△ADB是等边三角形,点C在△ADB的内部,DE⊥AC交直线AC于点E. 
(1)你能证明“DE=CE”吗?试一试;
(2)如图2,若点C在△ADB的外部时,即点D、E在AB两侧,上述结论是否还成立?说明理由. 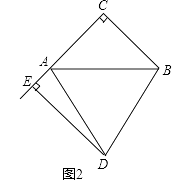
【答案】
(1)证明:如图1,过F作DF⊥BC,交BC延长线于F,则∠BFD=90°,
∵△ABD是等边三角形,
∴∠DAB=∠DBA=60°,AD=BD,
∵△ABC是等腰三角形,且∠ACB=90°,
∴∠CAB=∠CBA=45°,
∴∠DAC=∠DBF=60°﹣45°=15°,
∵DE⊥AC,
∴∠AED=90°,
∴∠AED=∠BFD,
∴△ADE≌△BDF,
∴DF=DE,
∵∠BFD=∠AED=∠FCE=90°,
∴四边形DFCE是矩形,
∵DE=DF,
∴矩形DFCE是正方形,
∴DE=CE
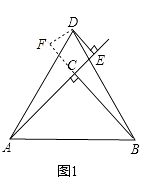
(2)证明:如图2,过D作DF⊥BC,交CB的延长线于F,则∠F=90°,
∵△ABD是等边三角形,
∴AD=BD,∠DAB=∠DBA=60°,
同理∠CAB=∠CBA=45°,
∴∠EAD=∠DBF=180°﹣60°﹣45°=75°,
∵∠AED=∠BFD=90°,
∴△AED≌△BFD,
∴DE=DF,
同理得:四边形DFCE是正方形,
∴DE=CE.
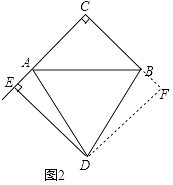
【解析】(1)如图1,作垂线,构建全等三角形,证明△ADE≌△BDF,得DF=DE,再证矩形DFCE是正方形,从而得出结论:DE=CE;(2)如图2,同理证明△AED≌△BFD和四边形DFCE是正方形,得出结论.
【考点精析】关于本题考查的等腰直角三角形和等边三角形的性质,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案