题目内容
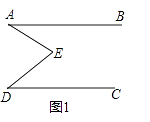
【题目】如图所示,直线AB, CD相交于点O,OF平分∠AOC,EO⊥CD于点O, 且∠DOF=160°,求∠BOE的度数;
【答案】解:∵∠DOF+∠COF=180°,∠DOF =160°
∴∠COF=180°—∠DOF=180°—160°= 20°
又∵OF平分∠AOC,
∴∠AOC=2∠COF=40°
∴∠DOB=∠AOC=40°
∵EO⊥CD,
∴∠DOE=90°
∴∠BOE=∠DOE+∠DOB=90°+40°=130°.
【解析】由已知∠DOF=160°,先求其邻补角∠COF,再利用OF平分∠AOC,求∠AOC,然后利用互余关系求∠AOE,最后利用邻补角关系求∠BOE.
【考点精析】关于本题考查的角的平分线和余角和补角的特征,需要了解从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;互余、互补是指两个角的数量关系,与两个角的位置无关才能得出正确答案.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
【题目】广州市某中学开展主题为“我爱阅读”的专题调查活动,了解学校1200名学生一年内阅读书籍的数量,随机抽取部分学生进行统计,绘制成如下尚未完成的频数分布表和频数分布直方图.请根据图表,解答下面的问题:
分组 | 频数 | 频率 |
0≤x<5 | 4 | 0.08 |
5≤x<10 | 14 | 0.28 |
10≤x<15 | 16 | a |
15≤x<20 | b | c |
20≤x<25 | 10 | 0.2 |
合计 | d | 1.00 |
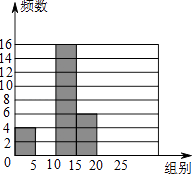
(1)a= , b= , c= , d= .
(2)补全频数分布直方图.
(3)根据该样本,估计该校学生阅读书籍数量在15本或以上的人数.
(4)如果阅读书籍数量在10本或以上的人数占总人数的70%以上,那么该校能评为“书香校园”,请根据上述数据分析该校是否能获得此荣誉,并说明理由.