题目内容
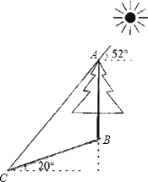
【题目】如图，在一个坡角为20°的斜坡上有一棵树，高为AB，当太阳光线与水平线成52°角时，测得该树斜坡上的树影BC的长为10m，求树高AB(精确到0.1m) (已知：sin20°≈0.342，cos20°≈0.940，tan20°≈0.364，sin52°≈0.788，cos52°≈0.616，tan52°≈1.280．供选用)
【答案】树高8.6米．
【解析】试题分析：过C作AB的垂线，设垂足为D．在Rt△CDB中，已知斜边BC=10m，利用三角函数求出CD和BD的长．同理在△ACD中，已知∠ACD=52°，CD，求出AD长，计算出AB=AD-BD，从而得到树的高度．
解：作CD⊥AB于D．
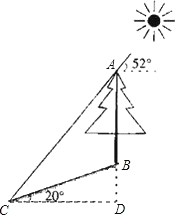
在Rt△BCD中，BC=10m，∠BCD=20°，
∴CD=BCcos20°≈10×0.940=9.40(m)，
BD=BCsin20°≈10×0.342=3.42(m)；
在Rt△ACD中，CD=9.40m，∠ACD=52°，
∴AD=CDtan52°≈9.40×1.280=12.032(m)．
∴AB=AD-BD=12.032-3.42≈8.6(m)．
答：树高8.6米．
练习册系列答案
相关题目
【题目】有这样一个问题：探究函数
的图象与性质．小华根据学习函数的经验，对函数的图象与性质进行了探究．下面是小华的探究过程，请补充完整：
(1)函数的自变量x的取值范围是___________；
(2)下表是y与x的几组对应值．m的值为_______；
x | -2 |
| -1 |
|
|
| 1 | 2 | 3 | 4 | … |
y | 0 |
| m |
|
|
|
| 1 |
|
| … |
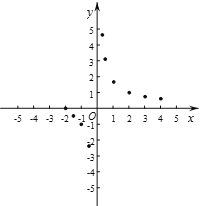
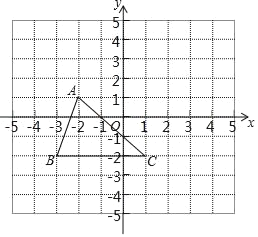
(3)如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
(4)结合函数的图象，写出该函数的一条性质：____________．
(5)结合函数图象估计
的解的个数为_______个．
