题目内容
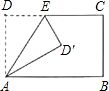将矩形ABCD沿AE折叠，得到如图所示的图形，已知∠CED′=60°，则∠BAD′的大小是30°
30°
．分析：利用翻折变换前后图形全等，推出∠DED′=120°，得∠DAD′=60°，所以∠BAD′=30°．
解答：解：∵如图所示△EDA≌△ED′A，
∴∠D=∠D′=∠DAE=90°，
∵∠CED′=60°，
∴∠DED′=120°，
∴∠DAD′=60°，
∴∠BAD′=30°．
故答案为：30°．
∴∠D=∠D′=∠DAE=90°，
∵∠CED′=60°，
∴∠DED′=120°，
∴∠DAD′=60°，
∴∠BAD′=30°．
故答案为：30°．
点评：本题主要考查了翻折变换的性质、正方形的性质、四边形内角和定理，解题的关键在于求出∠DAD′的度数．
练习册系列答案
阅读快车系列答案
相关题目
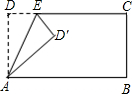将矩形ABCD沿AE折叠，得到如图所示的图形，已知∠CED′=60°，则∠AED的大小是（ ）| A、60° | B、50° | C、75° | D、55° |
将矩形ABCD沿AE折叠，得到如图所示的图形，已知∠CED′=60°，则∠EAB的大小是（ ）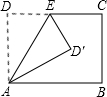
如图，将矩形ABCD沿AE折叠，若∠BAD′=30°，求∠AED′的度数．
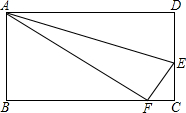如图，将矩形ABCD沿AE折叠，使点D落在BC边上的F处，已知AB=6，BC=10，则EC=