题目内容
 将矩形ABCD沿AE折叠,得到如图所示的图形,已知∠CED′=60°,则∠EAB的大小是( )
将矩形ABCD沿AE折叠,得到如图所示的图形,已知∠CED′=60°,则∠EAB的大小是( )分析:根据折叠前后的两个图形能够完全重合,再结合平角等于180°求出∠AED′的度数,然后求出∠AEC的度数,再根据两直线平行,同旁内角互补求解即可.
解答:解:由题意可得△ADE≌△AD′E,
∴∠AED=∠AED′,
∵∠CED′=60°,
∴∠AED′=
(180°-60°)=60°,
∴∠AEC=∠AED′+∠CED′=60°+60°=120°,
∵矩形ABCD,
∴AB∥CD,
∴∠EAB=180°-∠AEC=180°-120°=60°.
故选B.
∴∠AED=∠AED′,
∵∠CED′=60°,
∴∠AED′=
| 1 |
| 2 |
∴∠AEC=∠AED′+∠CED′=60°+60°=120°,
∵矩形ABCD,
∴AB∥CD,
∴∠EAB=180°-∠AEC=180°-120°=60°.
故选B.
点评:本题考查了角度的计算,矩形的对边平行,以及折叠的性质,根据折叠前后的两个图形能够完全重合得到∠AED=∠AED′是解决本题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
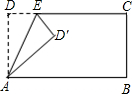 将矩形ABCD沿AE折叠,得到如图所示的图形,已知∠CED′=60°,则∠AED的大小是( )
将矩形ABCD沿AE折叠,得到如图所示的图形,已知∠CED′=60°,则∠AED的大小是( )| A、60° | B、50° | C、75° | D、55° |
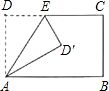 如图将矩形ABCD沿AE折叠,得到如图所示的图形,已知∠CED′=55°,则∠BAD′的大小是
如图将矩形ABCD沿AE折叠,得到如图所示的图形,已知∠CED′=55°,则∠BAD′的大小是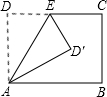 如图,将矩形ABCD沿AE折叠,若∠BAD′=30°,求∠AED′的度数.
如图,将矩形ABCD沿AE折叠,若∠BAD′=30°,求∠AED′的度数.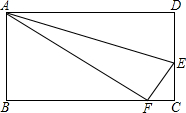 如图,将矩形ABCD沿AE折叠,使点D落在BC边上的F处,已知AB=6,BC=10,则EC=
如图,将矩形ABCD沿AE折叠,使点D落在BC边上的F处,已知AB=6,BC=10,则EC=