题目内容
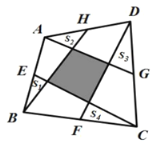
【题目】如图,![]() 分别为四边形
分别为四边形![]() 的边
的边![]() 的中点,并且图中四个小三角形的面积之和为
的中点,并且图中四个小三角形的面积之和为![]() ,即
,即![]() ,则图中阴影部分的面积为____.
,则图中阴影部分的面积为____.
【答案】1
【解析】
根据等底同高面积相等,找出面积相等的三角形并进行等量代换,得出S1+ S2+ S3+ S4与阴影部分的面积关系,继而得出阴影部分的面积.
解:如图,连接AC、BD,
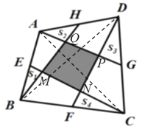
∵E、F、G、H分别为AB、BC、CD、DA的中点,
∴S△BCE=S△ACE,S△ADG=S△ACG,S△ABH=S△DBH,S△CDF=S△BDF,
∴S△BCE+ S△ADG=S△DBH+ S△BDF=![]() S四边形ABCD,
S四边形ABCD,
∴S1+ S四边形BMNF+ S4+ S2+ S四边形HQPD+ S3=S四边形BMNF+ S阴影+ S四边形HQPD,
∴S1+ S4+ S2+ S3=S阴影,
∵S1+ S2+ S3+ S4=1,
∴S阴影=1.
故答案为:1.

练习册系列答案
相关题目