题目内容
【题目】如图所示，正比例函数y= 
x的图象与反比例函数y= 
（k≠0）在第一象限的图象交于点 
，过点A作X轴的垂线，垂足为M，已知△AOM的面积为1．
（1）求反比例函数的解析式；
（2）如果点 
为反比例函数在第一象限图象上的点（点 与点 不重合），且点 的横坐标为1，在 
轴上求一点 
，使 
最小．
【答案】
（1）解：根据题意可设A点的坐标为（a，b），则b= 
．∴ab=k ．
∵△AOM的面积为1．
∴ 
ab=1 ，
∴ k=1 ．
∴ k=2．
∴ 反比例函数的解析式为y= 
（2）解：由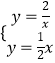 
得 
或 
，
∵A在第一象限，
∴ A为（2，1），设A点关于x轴的对称点为C，
则C点的坐标为（2，-1）如要在x轴上求一点P，使PA+PB最小．
则P点应为BC和x轴的交点，
如图所示．设直线BC的解析式为y=mx+n．
∵ B为（1，2），
∴ 
，解得： 
，
∴ BC的解析式为y=-3x+5．
当y=0时，-3x+5=0，x=-
,
∴ P点坐标为（ -，0）
【解析】（1）根据题意可设A点的坐标为（a，b），△AOM的面积为1，由反比例函数的k的几何意义，可得出ab=2，即|k|=2，k＞0，即可求出反比例函数的解析式。
（2）要在x轴上求作一点P，而A、B两点的x轴的同一侧，作点A关于x轴的对称点C，连接BC交x轴于点P，先求出点C和点B的坐标，再求出直线BC的函数解析式，然后求出当y=0时，x的值，即可求出点P饿坐标。
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识，掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法，以及对轴对称-最短路线问题的理解，了解已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径．
