题目内容
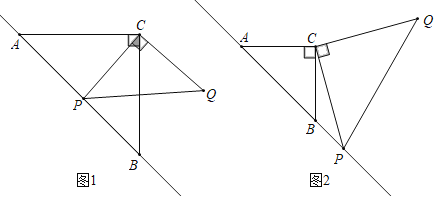
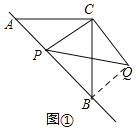
【题目】已知△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰Rt△PCQ,∠PCQ=90°.探究并解决下列问题:
(1)如图1,若点P在线段AB上,且AC=1+![]() ,PA=
,PA=![]() ,求线段PC的长.
,求线段PC的长.
(2)如图2,若点P在AB的延长线上,猜想PA2、PB2、PC2之间的数量关系,并证明.
(3)若动点P满足![]() ,则
,则![]() 的值为 .
的值为 .
【答案】(1)2;(2)AP2+BP2=PQ2.理由见解析;(3)![]() 或
或![]() .
.
【解析】
(1)在等腰直角三角形ACB中,由勾股定理先求得AB的长,然后根据PA的长,可求得PB的长;过点C作CD⊥AB,垂足为D,从而可求得CD、PD的长,然后在Rt三角形CDP中依据勾股定理可求得PC的长;
(2)过点C作CD⊥AB,垂足为D,则AP=(AD+PD)=(DC+PD),PB=(DP-BD)=(PD-DC),可证明AP2+BP2=2PC2,因为在Rt△PCQ中,PQ2=2CP2,所以可得出AP2+BP2=PQ2的结论;
(3)根据点P所在的位置画出图形,然后依据题目中的比值关系求得PD的长(用含有CD的式子表示),然后在Rt△ACP和Rt△DCP中由勾股定理求得AC和PC的长度即可.
解:(1)如图①所示:
∵△ABC是等腰直直角三角形,AC=![]() ,
,
∴AB=![]() ,
,
∵PA=![]() ,
,
∴PB=AB﹣PA=![]() ,
,
∵△ABC和△PCQ均为等腰直角三角形,
∴AC=BC,PC=CQ,∠ACB=∠PCQ,
∴∠ACP=∠BCQ,
在△APC和△BQC中,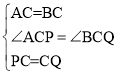 ,
,
∴△APC≌△BQC(SAS).
∴BQ=AP=![]() ,∠CBQ=∠A=45°.
,∠CBQ=∠A=45°.
∴△PBQ为直角三角形.
∴PQ=![]() .
.
∴PC=![]() PQ=2.
PQ=2.
故答案为:2;
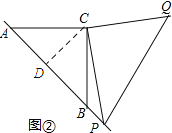
(2)AP2+BP2=PQ2.理由如下:
如图②:过点C作CD⊥AB,垂足为D.
∵△ACB为等腰直角三角形,CD⊥AB,
∴CD=AD=DB.
∵AP2=(AD+PD)2=(DC+PD)2=CD2+2DCPD+PD2,
PB2=(DP﹣BD)2=(PD﹣DC)2=DC2﹣2DCPD+PD2,
∴AP2+BP2=2CD2+2PD2,
∵在Rt△PCD中,由勾股定理可知:PC2=DC2+PD2,
∴AP2+BP2=2PC2.
∵△CPQ为等腰直角三角形,
∴2PC2=PQ2.
∴AP2+BP2=PQ2.
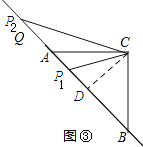
(3)如图③:过点C作CD⊥AB,垂足为D.
①当点P位于点P1处时.
![]() ,
,
![]() .
.
![]() .
.
在Rt△CP1D中,由勾股定理得: 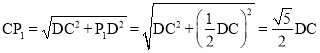 ,
,
在Rt△ACD中,由勾股定理得:![]() ,
,
![]() .
.
②当点P位于点P2处时.
![]() ,
,
∴P2A=![]() AB=DC.
AB=DC.
在Rt△CP2D中,由勾股定理得:![]() ,
,
在Rt△ACD中,由勾股定理得:![]() ,
,
![]() .
.
综上所述,![]() 的比值为
的比值为![]() 或
或![]() ;
;
故答案为:![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表:
时间(第x天) | 1 | 3 | 6 | 10 | … |
日销售量(m件) | 198 | 194 | 188 | 180 | … |
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
销售价格(元/件) | x+60 | 100 |
(1)求m关于x的一次函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格-每件成本)】
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
【题目】旺财水果店每天都会进一些草莓销售,在一周销售过程中他发现每天的销售量y(单位:千克)会随售价x(单位:元/千克)而变化,部分数据记录如表
售价x(单位:元/千克) | 30 | 25 | 20 |
每天销售量y(单位:千克) | 5 | 55 | 105 |
如果已知草莓每天销量y与售价x(30.5>x>14)满足一次函数关系.
(1)请根据表格中数据求出这个一次函数关系式;
(2)如果进价为14元/千克,请判断售价分别定为20元/千克和25元/千克,哪天的销售利润更高?
【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛,各参赛选手的成绩如下:
九(1)班:88,91,92,93,93,93,94,98,98,100;
九(2)班:89,93,93,93,95,96,96,98,98,99.
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
九(1)班 | 100 | m | 93 | 93 | 12 |
九(2)班 | 99 | 95 | n | p | 8.4 |
(1)直接写出表中m、n、p的值为:m=______,n=______,p=______;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好.”但也有人说(2)班的成绩要好.请给出两条支持九(2)班成绩更好的理由;
(3)学校确定了一个标准成绩,等于或大于这个成绩的学生被评定为“优秀”等级,如果九(2)班有一半的学生能够达到“优秀”等级,你认为标准成绩应定为______分,请简要说明理由.