题目内容
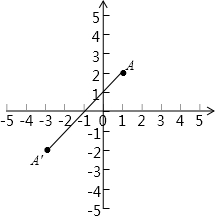
(1)点A(1,2)关于点P(-1,0)成中心对称的点的坐标为________;
(2)直线y=2x关于点P(-1,0)成中心对称的直线解析式为________;
(3)求直线y=2x-3绕点P(-1,0)顺时针旋转90°得到的直线解析式________.
解:(1)由图中可以看出A′的坐标为(-3,-2),故答案为(-3,-2);
(2)直线y=2x上的两点为A(0,0),B(1,2),
关于点P(-1,0)成中心对称的点为:A′(-2,0),B′(-3,-2),
设所求的解析式为y=kx+b,
 ,
,
解得k=2,b=4,
故答案为y=2x+4;

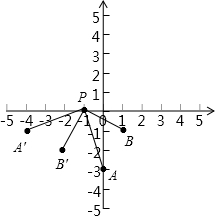
(3)易得原直线上两点为A(0,-3),B(1,-1),
关于点P(-1,0)顺时针旋转90°得到的A′(-4,-1),B′(-2,-2),
设所求的解析式为y=kx+b,
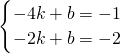 ,
,
解得k=- ,b=-3,
,b=-3,
故答案为:y=- k-3.
k-3.
分析:(1)连接AP并延长到A′,使A′P=AP,看P′的坐标即可;
(2)先得到原直线上的任意两点,进而找到关于点P(-1,0)成中心对称的两点,代入直线解析式可得所求的直线解析式;
(3)先得到原直线上的任意两点,进而找到关于点P(-1,0)顺时针旋转90°得到的两点,代入一次函数可得相关解析式.
点评:本题考查了图形旋转的性质,得到经过旋转后的对应点是解决本题的关键;求函数解析式一般要用待定系数法.

(2)直线y=2x上的两点为A(0,0),B(1,2),
关于点P(-1,0)成中心对称的点为:A′(-2,0),B′(-3,-2),
设所求的解析式为y=kx+b,
 ,
,解得k=2,b=4,
故答案为y=2x+4;

(3)易得原直线上两点为A(0,-3),B(1,-1),
关于点P(-1,0)顺时针旋转90°得到的A′(-4,-1),B′(-2,-2),
设所求的解析式为y=kx+b,

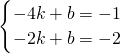 ,
,解得k=-
 ,b=-3,
,b=-3,故答案为:y=-
 k-3.
k-3.分析:(1)连接AP并延长到A′,使A′P=AP,看P′的坐标即可;
(2)先得到原直线上的任意两点,进而找到关于点P(-1,0)成中心对称的两点,代入直线解析式可得所求的直线解析式;
(3)先得到原直线上的任意两点,进而找到关于点P(-1,0)顺时针旋转90°得到的两点,代入一次函数可得相关解析式.
点评:本题考查了图形旋转的性质,得到经过旋转后的对应点是解决本题的关键;求函数解析式一般要用待定系数法.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
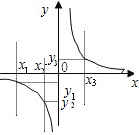 在函数y=
在函数y=| k |
| x |
| A、y1<0<y2 |
| B、y3<0<y1 |
| C、y2<y1<y3 |
| D、y3<y1<y2 |
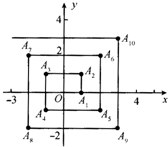 9、如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),则点A2008的坐标为
9、如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),则点A2008的坐标为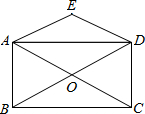 23、如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.
23、如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.