题目内容
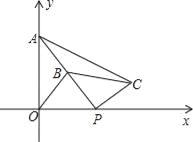
【题目】如图所示,抛物线y=ax2+bx+c与直线y=﹣x+6分别交于x轴和y轴上同一点,交点分别是点B和点C,且抛物线的对称轴为直线x=4.
(1)求出抛物线与x轴的两个交点A,B的坐标.
(2)试确定抛物线的解析式.

【答案】(1)A(2,0),B(6,0);(2)![]()
【解析】分析: (1)根据抛物线y= ![]() 与直线y=-x+6分别交于x轴和y轴上同一点,交点分别是点B和点C,可以求得点B、C两点的坐标,由图象可知抛物线y=
与直线y=-x+6分别交于x轴和y轴上同一点,交点分别是点B和点C,可以求得点B、C两点的坐标,由图象可知抛物线y= ![]() 与x轴交于点A、B两点,对称轴为直线x=4,从而可以求得点A的坐标;
与x轴交于点A、B两点,对称轴为直线x=4,从而可以求得点A的坐标;
(2)根据抛物线过点A、B、C三点,从而可以求得抛物线的解析式.
本题解析:(1)∵抛物线y= ![]() 与直线y=﹣x+6分别交于x轴和y轴上同一点,交点分别是点B和点C,
与直线y=﹣x+6分别交于x轴和y轴上同一点,交点分别是点B和点C,
∴将x=0代入y=﹣x+6得,y=6;
将y=0代入y=﹣x+6,得x=6.
∴点B的坐标是(6,0),点C的坐标是(0,6).∵抛物线y= ![]() 与x轴交于点A、B两点,对称轴为直线x=4,
与x轴交于点A、B两点,对称轴为直线x=4,
∴点A的坐标为(2,0)
即抛物线与x轴的两个交点A,B的坐标分别是(2,0),(6,0).
(2)∵抛物线y= ![]() 过点A(2,0),B(6,0),C(0,6),
过点A(2,0),B(6,0),C(0,6),
∴解得a= ![]() ,b=﹣4,c=6∴抛物线的解析式为:y=
,b=﹣4,c=6∴抛物线的解析式为:y=![]()
考点:抛物线与坐标轴的交点

练习册系列答案
相关题目