题目内容
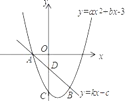
【题目】如图![]() ,抛物线
,抛物线![]() :
:![]() 经过原点
经过原点![]() ,与x轴的另一个交点为
,与x轴的另一个交点为![]() ,将抛物线
,将抛物线![]() 向右平移
向右平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,
,![]() 交x轴于A、B两点
交x轴于A、B两点![]() 点A在点B的左边
点A在点B的左边![]() ,交y轴于点C.
,交y轴于点C.
![]() 求抛物线
求抛物线![]() 的解析式.
的解析式.
![]() 如图
如图![]() ,当
,当![]() 时,连接AC,过点A做
时,连接AC,过点A做![]() 交抛物线
交抛物线![]() 于点D,连接CD.
于点D,连接CD.
![]() 求抛物线
求抛物线![]() 的解析式.
的解析式.
![]() 直接写出点D的坐标为______.
直接写出点D的坐标为______.
![]() 若抛物线
若抛物线![]() 的对称轴上存在点P,使
的对称轴上存在点P,使![]() 为等边三角形,请直接写出此时m的值.
为等边三角形,请直接写出此时m的值.

【答案】(1)抛物线![]() 的解析式为:
的解析式为:![]() (2)
(2)![]() ;②点D的坐标为
;②点D的坐标为![]() ;(3)存在点P,使
;(3)存在点P,使![]() 为等边三角形,此时m的值为
为等边三角形,此时m的值为![]() ,理由见解析
,理由见解析
【解析】
![]() 把原点
把原点![]() 与
与![]() 代入抛物线
代入抛物线![]() :
:![]() ,解方程组求得b,c的值,即可得出抛物线
,解方程组求得b,c的值,即可得出抛物线![]() 的解析式;
的解析式;
![]() 根据抛物线的平移规律可得抛物线
根据抛物线的平移规律可得抛物线![]() 的解析式;
的解析式;
![]() 由抛物线
由抛物线![]() 的解析式,求得点
的解析式,求得点![]() ,
,![]() ,
,![]() ,作
,作![]() 轴于点H,设点
轴于点H,设点![]() ,证明
,证明![]() ∽
∽![]() ,得
,得![]() ,求得点D的横坐标,再代入抛物线求得纵坐标,即可得出点D的坐标;
,求得点D的横坐标,再代入抛物线求得纵坐标,即可得出点D的坐标;
![]() 设抛物线
设抛物线![]() 的解析式为:
的解析式为:![]() ,可得
,可得![]() ,
,![]() ,对称轴为直线
,对称轴为直线![]() ,延长AP至K,使
,延长AP至K,使![]() ,连接KC,作
,连接KC,作![]() 轴于G,证明
轴于G,证明![]() ∽
∽![]() ,可得
,可得![]() ,利用中点坐标公式得出点P的横坐标为:
,利用中点坐标公式得出点P的横坐标为:![]() ,所以
,所以![]() ,解方程即可得出m的值.
,解方程即可得出m的值.
![]() 抛物线
抛物线![]() :
:![]() 经过原点
经过原点![]() ,与x轴的另一个交点为
,与x轴的另一个交点为![]() ,
,
![]() ,解得
,解得![]() ,
,
![]() 抛物线
抛物线![]() 的解析式为:
的解析式为:![]() ;
;
![]() ,
,
当![]() 时,抛物线
时,抛物线![]() 的解析式为:
的解析式为:![]() ;
;
![]() 当
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() 或
或![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
如图,作![]() 轴于点H,设点
轴于点H,设点![]() ,
,
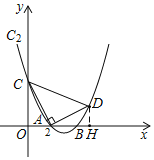
![]() ,
,
![]() ,
,
![]() ,
,
![]() ∽
∽![]()
![]() ,即
,即![]() ,
,
解得![]() ,此时
,此时![]() ,
,
![]() 点D的坐标为
点D的坐标为![]() ,
,
故答案为:![]() ,
,
![]() 由题意,抛物线
由题意,抛物线![]() 的解析式为:
的解析式为:![]() ,
,
![]() ,
,![]() ,对称轴为直线
,对称轴为直线![]() ,
,
延长AP至K,使![]() ,连接KC,作
,连接KC,作![]() 轴于G,
轴于G,
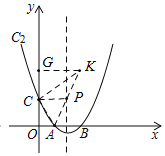
![]() 为等边三角形,
为等边三角形,
![]() ,
,
![]() ,
,
同理可证![]() ∽
∽![]() ,
,
![]() ,
,
![]() ,
,
即点K的横坐标为:![]() ,
,
![]() 点P的横坐标为:
点P的横坐标为:![]() ,
,
![]() ,
,
化简,得![]() ,
,
![]() ,
,
![]() 或
或![]() 舍去
舍去![]() ,
,
![]() 存在点P,使
存在点P,使![]() 为等边三角形,此时m的值为
为等边三角形,此时m的值为![]() .
.

练习册系列答案
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目