题目内容
【题目】对于一个关于x的代数式A,若存在一个系数为正数关于x的单项式F,使![]() 的结果是所有系数均为整数的整式,则称单项式F为代数式A的“整系单项式”.例如:
的结果是所有系数均为整数的整式,则称单项式F为代数式A的“整系单项式”.例如:
当A=![]() ,F=2x3时,由于
,F=2x3时,由于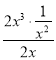 =1,故2x3是
=1,故2x3是![]() 的整系单项式;
的整系单项式;
当A=![]() ,F=6x5时,由于
,F=6x5时,由于 ,故6x5是
,故6x5是![]() 的整系单项式;
的整系单项式;
当A=3-![]() ,F=
,F=![]() 时,由于
时,由于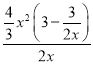 =2x-1,故
=2x-1,故![]() 是3-
是3-![]() 的整系单项式;
的整系单项式;
当A=3-![]() ,F=8x4时,由于
,F=8x4时,由于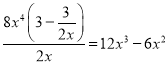 ,故8x4是3-
,故8x4是3-![]() 的整系单项式;
的整系单项式;
显然,当代数式A存在整系单项式F时,F有无数个,现把次数最低,系数最小的整系单项式F记为F(A).例如:![]() ,
,![]()
阅读以上材料并解决下列问题:
(1)判断:当A=![]() 时,F=2x3______A的整系单项式(填“是”或“不是”)
时,F=2x3______A的整系单项式(填“是”或“不是”)
(2)解方程: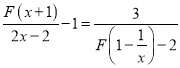
(3)已知a、b、c是△ABC的边长,其中a、b满足(a-5)2+![]() =0,且关于x的方程|
=0,且关于x的方程|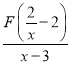 |=c有且只有3个不相等的实数根,求△ABC的周长.
|=c有且只有3个不相等的实数根,求△ABC的周长.
【答案】(1)是;(2)x=![]() ;(3)26或27;
;(3)26或27;
【解析】
(1)当A=![]() 时,F=2x3时,
时,F=2x3时,![]() =x;
=x;
(2)令F=axn,结合定义进行判断,即可求出F(x+1)=2x,F(1-![]() )=2x2,将所求方程转化为
)=2x2,将所求方程转化为![]() -1=
-1=![]() 即可求解;
即可求解;
(3)根据平方与二次根式的性质可求a=5,b=9,再求出F(![]() )=x2,将所求式子转化为可以化为|
)=x2,将所求式子转化为可以化为|![]() |=c,结合函数图象即可求解;
|=c,结合函数图象即可求解;
解:(1)当A=![]() 时,F=2x3时,
时,F=2x3时,![]() =x,
=x,
∴![]() 是2x3的整系单项式;
是2x3的整系单项式;
(2)F(x+1)=2x,F(1-![]() )=2x2,
)=2x2,
∴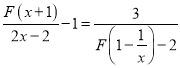 可以化为
可以化为![]() -1=
-1=![]() ,
,
∴2x2-3x+1=0,
∴x=1或x=![]() ;
;
经检验x=1是方程的增根,
∴原方程的解为x=![]() ;
;
(3)∵(a-5)2+![]() =0,
=0,
∴a=5,b=9,
F(![]() )=x2,
)=x2,
∴|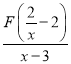 |=c可以化为|
|=c可以化为|![]() |=c,
|=c,
∴|(x-3)+![]() +6|=c,
+6|=c,
当x=6时,c=12,
∴当x≥6时,c≥12,此时方程有且只有3个不相等的实数根,
∵c<14,
∴c=12或c=13,
∴△ABC的周长为26或27;

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案