题目内容
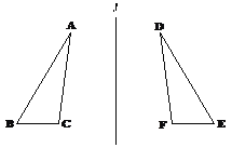
【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.

【答案】(1)证明见解析;(2)4.
【解析】
试题分析:(1)由AE=DF,∠A=∠D,AB=DC,易证得△AEC≌△DFB,即可得BF=EC,∠ACE=∠DBF,且EC∥BF,即可判定四边形BFCE是平行四边形;
(2)当四边形BFCE是菱形时,BE=CE,根据菱形的性质即可得到结果.
试题解析:(1)∵AB=DC,∴AC=DB,
在△AEC和△DFB中 ,∴△AEC≌△DFB(SAS),
,∴△AEC≌△DFB(SAS),
∴BF=EC,∠ACE=∠DBF,∴EC∥BF,∴四边形BFCE是平行四边形;
(2)当四边形BFCE是菱形时,BE=CE,∵AD=10,DC=3,AB=CD=3,
∴BC=10﹣3﹣3=4,∵∠EBD=60°,∴BE=BC=4,
∴当BE=4 时,四边形BFCE是菱形,
故答案为:4.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目