题目内容
在直角坐标系中,已知点A(-3,2),B(2,-4),在x轴上找一点C,使AC+BC最短,则点C的坐标为( )
A、(0,-
| ||
B、(-
| ||
| C、(-4,0) | ||
D、(
|
分析:点A(-3,2)在第二象限,点B(2,-4)在第四象限,连接AB交x轴于C点,C点即为所求.根据A、B两点的坐标求直线AB的解析式,再求C点坐标.
解答:解:设直线AB解析式为y=kx+b,
将A(-3,2),B(2,-4)代入,得
,
解得
,
∴y=-
x-
,
当y=0时,x=-
,
即C(-
,0).
故选B.
将A(-3,2),B(2,-4)代入,得
|
解得
|
∴y=-
| 6 |
| 5 |
| 8 |
| 5 |
当y=0时,x=-
| 4 |
| 3 |
即C(-
| 4 |
| 3 |
故选B.
点评:本题考查了坐标系中求最短路线问题.当已知两点在x轴两侧时,直接连接这两点,与x轴的交点即为所求;当已知两点在x轴同侧时,作其中一个点关于x轴的对称点,将对称点与另外一个点连接,与x轴的交点即为所求.

练习册系列答案
相关题目
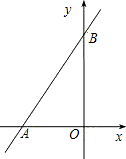 如图,在直角坐标系中,已知直线y=kx+6与x轴、y轴分别交于A、B两点,且△ABO的面积为12.
如图,在直角坐标系中,已知直线y=kx+6与x轴、y轴分别交于A、B两点,且△ABO的面积为12.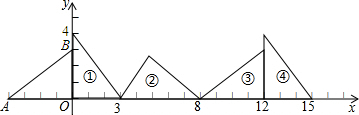
 的直角顶点的坐标为
的直角顶点的坐标为