题目内容
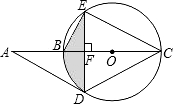
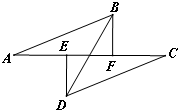 18、如图,点A、E、F、C在一条直线上,若将△DEC的边EC沿AC方向平移,平移过程中始终满足下列条件:AE=CF,DE⊥AC于E,BF⊥AC于F,且AB=CD.则当点E、F不重合时,BD与EF的关系是
18、如图,点A、E、F、C在一条直线上,若将△DEC的边EC沿AC方向平移,平移过程中始终满足下列条件:AE=CF,DE⊥AC于E,BF⊥AC于F,且AB=CD.则当点E、F不重合时,BD与EF的关系是互相平分
.分析:由已知可推出AE+EF=CF+EF,DE⊥AC于E,BF⊥AC于F推出∠DEC=∠BFA=90°,AB=CD,所以推出△ABF≌CDE,则DE=BF,所以证得△DOE≌△BOF,则得:OE=OF,OB=OD.
解答:解:已知AE=CF,DE⊥AC于E,BF⊥AC于F,且AB=CD且点E、F不重合,
∴AE+EF=CF+EF,即AF=CE,
∴∠DEC=∠BFA=90°,
又已知AB=CD,
∴△ABF≌CDE,
∴DE=BF,
∠DOE=∠BOF,
∴△DOE≌△BOF,
∴OE=OF,OB=OD,
∴BD和EF互相平分.
故答案为:互相平分.
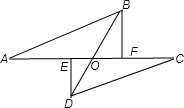
∴AE+EF=CF+EF,即AF=CE,
∴∠DEC=∠BFA=90°,
又已知AB=CD,
∴△ABF≌CDE,
∴DE=BF,
∠DOE=∠BOF,
∴△DOE≌△BOF,
∴OE=OF,OB=OD,
∴BD和EF互相平分.
故答案为:互相平分.

点评:此题考查的知识点是平行四边形的判定和性质、全等三角形的判定和性质,关键是由已知证△ABF≌CDE和△DOE≌△BOF得出结论.

练习册系列答案
相关题目
 如图,点A的坐标为(2
如图,点A的坐标为(2| 2 |
| A、(0,0) | ||||||||
B、(
| ||||||||
| C、(1,1) | ||||||||
D、(
|
 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°.
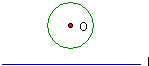 12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是
12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是