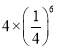ЬтФПФкШн
ЁОЬтФПЁПзлКЯЬНОП
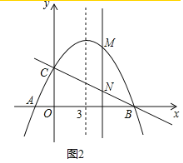
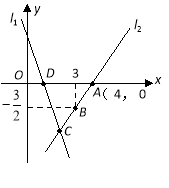
вбжЊХзЮяЯпyЃНax2+![]() x+4ЕФЖдГЦжсЪЧжБЯпxЃН3ЃЌгыxжсЯрНЛгкAЃЌBСНЕуЃЈЕуBдкЕуAгвВрЃЉЃЌгыyжсНЛгкЕуCЃЎ
x+4ЕФЖдГЦжсЪЧжБЯпxЃН3ЃЌгыxжсЯрНЛгкAЃЌBСНЕуЃЈЕуBдкЕуAгвВрЃЉЃЌгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНКЭAЃЌBСНЕуЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌШєЕуPЪЧХзЮяЯпЩЯBЁЂCСНЕужЎМфЕФвЛИіЖЏЕуЃЈВЛгыBЁЂCжиКЯЃЉЃЌЪЧЗёДцдкЕуPЃЌЪЙЫФБпаЮPBOCЕФУцЛ§зюДѓЃПШєДцдкЃЌЧѓЕуPЕФзјБъМАЫФБпаЮPBOCУцЛ§ЕФзюДѓжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌШєЕуMЪЧХзЮяЯпЩЯШЮвтвЛЕуЃЌЙ§ЕуMзїyжсЕФЦНааЯпЃЌНЛжБЯпBCгкЕуNЃЌЕБMNЃН3ЪБЃЌжБНгаДГіЕуMЕФзјБъЃЎ
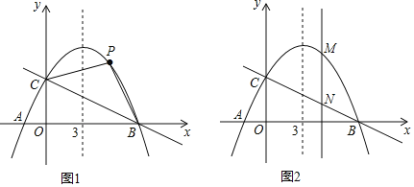
ЁОД№АИЁПЃЈ1ЃЉХзЮяЯпЕФНтЮіЪНЮЊЃКyЃНЉ![]() x2+
x2+![]() x+4ЃЛЕуAЕФзјБъЮЊ(Љ2ЃЌ0)ЃЌЕуBЕФзјБъЮЊ(8ЃЌ0)ЃЈ2ЃЉДцдкЕуP(4ЃЌ6)ЃЌЪЙЕУЫФБпаЮPBOCЕФУцЛ§зюДѓЃЛЕуPЕФзјБъЮЊ(4ЃЌ6)ЃЌЫФБпаЮPBOCУцЛ§ЕФзюДѓжЕЮЊ32ЃЈ3ЃЉЕуMЕФзјБъЮЊ(2ЃЌ6)ЁЂ(6ЃЌ4)ЁЂ(4Љ2
x+4ЃЛЕуAЕФзјБъЮЊ(Љ2ЃЌ0)ЃЌЕуBЕФзјБъЮЊ(8ЃЌ0)ЃЈ2ЃЉДцдкЕуP(4ЃЌ6)ЃЌЪЙЕУЫФБпаЮPBOCЕФУцЛ§зюДѓЃЛЕуPЕФзјБъЮЊ(4ЃЌ6)ЃЌЫФБпаЮPBOCУцЛ§ЕФзюДѓжЕЮЊ32ЃЈ3ЃЉЕуMЕФзјБъЮЊ(2ЃЌ6)ЁЂ(6ЃЌ4)ЁЂ(4Љ2![]() ЃЌ
ЃЌ![]() Љ1)Лђ(4+2
Љ1)Лђ(4+2![]() ЃЌЉ
ЃЌЉ![]() Љ1)
Љ1)
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнХзЮяЯпЕФЖдГЦжсЗНГЬЃЌМДПЩЕУЕНaЕФжЕЃЌДгЖјЕУЕНКЏЪ§НтЮіЪНЃЌНјЖјЧѓГіAЃЌBЕФжЕЃЛ
ЃЈ2ЃЉИљОнД§ЖЈЯЕЪ§ЗЈЃЌЧѓГіжБЯпBCЕФНтЮіЪНЃЌЩшЕуPЕФзјБъЮЊЃЈxЃЌЉ![]() x2+
x2+![]() x+4ЃЉЃЌЙ§ЕуPзїPDЁЮyжсЃЌНЛжБЯпBCгкЕуDЃЌдђЕуDЕФзјБъЮЊ(xЃЌЉ
x+4ЃЉЃЌЙ§ЕуPзїPDЁЮyжсЃЌНЛжБЯпBCгкЕуDЃЌдђЕуDЕФзјБъЮЊ(xЃЌЉ![]() x+4)ЃЌНјЖјЧѓГіPDЕФжЕЃЌИљОнSЫФБпаЮPBOCЃНSЁїBOC+SЁїPBCЃЌЕУЕНЖўДЮКЏЪ§НтЮіЪНЃЌМДПЩЕУЕНД№АИЃЛ
x+4)ЃЌНјЖјЧѓГіPDЕФжЕЃЌИљОнSЫФБпаЮPBOCЃНSЁїBOC+SЁїPBCЃЌЕУЕНЖўДЮКЏЪ§НтЮіЪНЃЌМДПЩЕУЕНД№АИЃЛ
ЃЈ3ЃЉЩшЕуMЕФзјБъЮЊ(mЃЌЉ![]() m2+
m2+![]() m+4)ЃЌдђЕуNЕФзјБъЮЊ(mЃЌЉ
m+4)ЃЌдђЕуNЕФзјБъЮЊ(mЃЌЉ![]() m+4)ЃЌдђMN=|Љ
m+4)ЃЌдђMN=|Љ![]() m2+2m |ЃЌИљОнMN=3ЃЌСаГіЙигкmЕФЗНГЬЃЌМДПЩЧѓНтЃЎ
m2+2m |ЃЌИљОнMN=3ЃЌСаГіЙигкmЕФЗНГЬЃЌМДПЩЧѓНтЃЎ
ЃЈ1ЃЉЁп ХзЮяЯпЕФЖдГЦжсЪЧЃКжБЯпxЃН3ЃЌ
Ёр ![]() ЃН3ЃЌНтЕУЃКaЃНЉ
ЃН3ЃЌНтЕУЃКaЃНЉ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃКyЃНЉ![]() x2+
x2+![]() x+4ЃЎ
x+4ЃЎ
ЕБyЃН0ЪБЃЌЉ![]() x2+
x2+![]() x+4ЃН0ЃЌНтЕУx1ЃНЉ2ЃЌx2ЃН8ЃЌ
x+4ЃН0ЃЌНтЕУx1ЃНЉ2ЃЌx2ЃН8ЃЌ
ЁрЕуAЕФзјБъЮЊ(Љ2ЃЌ0)ЃЌЕуBЕФзјБъЮЊ(8ЃЌ0)ЃЛ
ЃЈ2ЃЉЕБxЃН0ЪБЃЌyЃНЉ![]() x2+
x2+![]() x+4ЃН4ЃЌ
x+4ЃН4ЃЌ
ЁрЕуCЕФзјБъЮЊ(0ЃЌ4)ЃЎ
ЩшжБЯпBCЕФНтЮіЪНЮЊЃКyЃНkx+bЃЈkЁй0ЃЉЃЌ
НЋB(8ЃЌ0)ЃЌC(0ЃЌ4)ДњШыyЃНkx+bЕУЃК![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК ЃЌ
ЃЌ
ЁржБЯпBCЕФНтЮіЪНЮЊЃКyЃНЉ![]() x+4ЃЎ
x+4ЃЎ
МйЩшДцдкЕуPЃЌЪЙЫФБпаЮPBOCЕФУцЛ§зюДѓЃЌ
ЩшЕуPЕФзјБъЮЊЃЈxЃЌЉ![]() x2+
x2+![]() x+4ЃЉЃЌШчЭМ1ЃЌ
x+4ЃЉЃЌШчЭМ1ЃЌ
Й§ЕуPзїPDЁЮyжсЃЌНЛжБЯпBCгкЕуDЃЌдђЕуDЕФзјБъЮЊ(xЃЌЉ![]() x+4)ЃЌ
x+4)ЃЌ
ЁрPDЃНЉ![]() x2+
x2+![]() x+4Љ(Љ
x+4Љ(Љ![]() x+4)ЃНЉ
x+4)ЃНЉ![]() x2+2xЃЌ
x2+2xЃЌ
ЁрSЫФБпаЮPBOCЃНSЁїBOC+SЁїPBCЃН![]() ЁС8ЁС4+
ЁС8ЁС4+![]() PDOB
PDOB
ЃН16+![]() ЁС8(Љ
ЁС8(Љ![]() x2+2x)ЃНЉx2+8x+16
x2+2x)ЃНЉx2+8x+16
ЃНЉЃЈxЉ4ЃЉ2+32
ЁрЕБxЃН4ЪБЃЌЫФБпаЮPBOCЕФУцЛ§зюДѓЃЌзюДѓжЕЪЧ32ЃЎ
Ёп0ЃМxЃМ8ЃЌ
ЁрДцдкЕуP(4ЃЌ6)ЃЌЪЙЕУЫФБпаЮPBOCЕФУцЛ§зюДѓЃЌЫФБпаЮPBOCУцЛ§ЕФзюДѓжЕЮЊ32ЃЎ
ЃЈ3ЃЉЩшЕуMЕФзјБъЮЊ(mЃЌЉ![]() m2+
m2+![]() m+4)ЃЌдђЕуNЕФзјБъЮЊ(mЃЌЉ
m+4)ЃЌдђЕуNЕФзјБъЮЊ(mЃЌЉ![]() m+4)ЃЌШчЭМ2ЃЌ
m+4)ЃЌШчЭМ2ЃЌ
ЁрMNЃН|Љ![]() m2+
m2+![]() m+4Љ(Љ
m+4Љ(Љ![]() m+4)|ЃН|Љ
m+4)|ЃН|Љ![]() m2+2m |ЃЌ
m2+2m |ЃЌ
гжЁп MNЃН3ЃЌ
Ёр |Љ![]() m2+2m |ЃН3ЃЌ
m2+2m |ЃН3ЃЌ
ЕБ0ЃМmЃМ8ЪБЃЌЉ![]() m2+2mЉ3ЃН0ЃЌНтЕУЃКm1ЃН2ЃЌm2ЃН6ЃЌ
m2+2mЉ3ЃН0ЃЌНтЕУЃКm1ЃН2ЃЌm2ЃН6ЃЌ
ЁрЕуMЕФзјБъЮЊ(2ЃЌ6)Лђ(6ЃЌ4)ЃЛ
ЕБmЃМ0ЛђmЃО8ЪБЃЌЉ![]() m2+2m +3ЃН0ЃЌНтЕУЃКm3ЃН4Љ2
m2+2m +3ЃН0ЃЌНтЕУЃКm3ЃН4Љ2![]() ЃЌm4ЃН4+2
ЃЌm4ЃН4+2![]() ЃЌ
ЃЌ
ЁрЕуMЕФзјБъЮЊ(4Љ2![]() ЃЌ
ЃЌ![]() Љ1)Лђ(4+2
Љ1)Лђ(4+2![]() ЃЌЉ
ЃЌЉ![]() Љ1)ЃЎ
Љ1)ЃЎ
Д№ЃКЕуMЕФзјБъЮЊ(2ЃЌ6ЃЉЁЂ(6ЃЌ4ЃЉЁЂ(4Љ2![]() ЃЌ
ЃЌ![]() Љ1ЃЉЛђ(4+2
Љ1ЃЉЛђ(4+2![]() ЃЌЉ
ЃЌЉ![]() Љ1ЃЉЃЎ
Љ1ЃЉЃЎ