题目内容
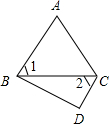 如图,在△ABC和△DBC中,∠A=50°,∠2=∠1,则∠ACD的度数是
如图,在△ABC和△DBC中,∠A=50°,∠2=∠1,则∠ACD的度数是
- A.50°
- B.120°
- C.130°
- D.无法确定
C
分析:由∠2=∠1得AB∥CD,所以得∠A+∠ACD=180°,从而求出∠ACD的度数.
解答:∵∠2=∠1,
∴AB∥CD,
∴∠A+∠ACD=180,
∴∠ACD=180°-50°=130°.
故选:C.
点评:此题考查的知识点是平行线的判定与性质,关键是先由∠2=∠1得AB∥CD,再由两直线平行,同旁内角互补求出∠ACD的度数.
分析:由∠2=∠1得AB∥CD,所以得∠A+∠ACD=180°,从而求出∠ACD的度数.
解答:∵∠2=∠1,
∴AB∥CD,
∴∠A+∠ACD=180,
∴∠ACD=180°-50°=130°.
故选:C.
点评:此题考查的知识点是平行线的判定与性质,关键是先由∠2=∠1得AB∥CD,再由两直线平行,同旁内角互补求出∠ACD的度数.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
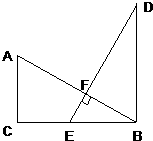 22、已知,如图,在△ABC和△EDB中,∠ACB=∠EBD=90°,点E在BC上,DE⊥AB交AB于F,且AB=ED.求证:DB=BC.
22、已知,如图,在△ABC和△EDB中,∠ACB=∠EBD=90°,点E在BC上,DE⊥AB交AB于F,且AB=ED.求证:DB=BC.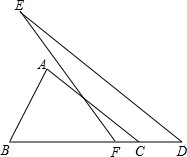 如图,在△ABC和△DEF中,AC∥DE,∠EFD与∠B互补,DE=mAC(m>1).试探索线段EF与AB的数量关系,并证明你的结论.
如图,在△ABC和△DEF中,AC∥DE,∠EFD与∠B互补,DE=mAC(m>1).试探索线段EF与AB的数量关系,并证明你的结论.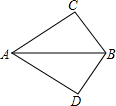 如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“AAS”证明△ABC≌△ABD,则需要加条件
如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“AAS”证明△ABC≌△ABD,则需要加条件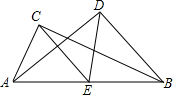 如图,在△ABC和△ABD中,AC⊥BC,AD⊥BD,E是AB边上的中点.则DE
如图,在△ABC和△ABD中,AC⊥BC,AD⊥BD,E是AB边上的中点.则DE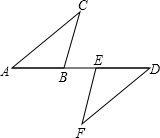 如图,在△ABC和△DEF中,∠A=∠D,∠C=∠F,AC=DF,请说明AE=BD的理由.
如图,在△ABC和△DEF中,∠A=∠D,∠C=∠F,AC=DF,请说明AE=BD的理由.