题目内容
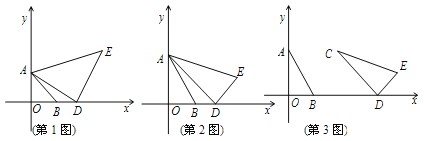
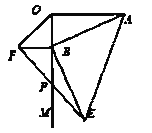
【题目】如图,AO![]() OM,OA=4,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF.等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,则PB的长度为_________.
OM,OA=4,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF.等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,则PB的长度为_________.
【答案】2.
【解析】试题分析:作辅助线,首先证明△ABO≌△BEN,得到BO=ME;进而证明△BPF≌△MPE,即可解决问题.如图,过点E作EN⊥BM,垂足为点N,∵∠AOB=∠ABE=∠BNE=90°,∴∠ABO+∠BAO=∠ABO+∠NBE=90°,∴∠BAO=∠NBE,∵△ABE、△BFO均为等腰直角三角形,∴AB=BE,BF=BO;在△ABO与△BEN中,∠BAO=∠NBE,∠AOB=∠BNE,AB=BE,∴△ABO≌△BEN(AAS),∴BO=NE,BN=AO;∵BO=BF,∴BF=NE,在△BPF与△NPE中,∠FBP=∠ENP,∠FPB=∠EPN,BF=NE,∴△BPF≌△NPE(AAS),∴BP=NP=![]() BN;而BN=AO,∴BP=
BN;而BN=AO,∴BP=![]() AO=
AO=![]() ×4=2.
×4=2.
故答案为:2.


练习册系列答案
相关题目