题目内容
【题目】综合与实践
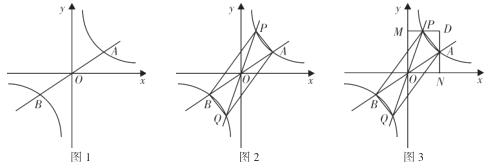
如图1,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 、
、![]() .我们可以发现:反比例函数
.我们可以发现:反比例函数![]() 的图象是一个关于原点中心对称的图形.
的图象是一个关于原点中心对称的图形.
(1)填空:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)利用所给函数图象,写出不等式![]() 的解集 ;
的解集 ;
(3)如图2,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 、
、![]() .试说明以
.试说明以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形一定是平行四边形,但不可能是正方形;
为顶点的四边形一定是平行四边形,但不可能是正方形;
(4)如图3,当点![]() 在点
在点![]() 的左上方时,过
的左上方时,过![]() 作直线
作直线![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线
作直线轴于点
![]() ,交直线
,交直线![]() 于点
于点![]() ,若四边形
,若四边形![]() 的面积为
的面积为![]() .求点
.求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;
;![]() ;
;![]() ;
;![]() ;(2)
;(2)![]() 或
或![]() ;(3)见解析;(4)点
;(3)见解析;(4)点![]() 的坐标为
的坐标为![]()
【解析】
(1)由题意直接把点A(3,2)代入一次函数及反比例函数的解析式求出k1及a的值,再根据反比例函数的图象关于原点对称可得出m、n的值;
(2)由题意直接根据两函数的图象即可得出结论;
(3)根据题意利用“反比例函数的图象是一个关于原点中心对称的图形”得:OA=OB,OP=OQ,故以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形的对角线互相平分,所以以
为顶点的四边形的对角线互相平分,所以以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形一定是平行四边形,并由
为顶点的四边形一定是平行四边形,并由![]() ,对角线
,对角线![]() 与
与![]() 不可能互相垂直,即可得出以
不可能互相垂直,即可得出以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形不可能是菱形,也就不可能是正方形;
为顶点的四边形不可能是菱形,也就不可能是正方形;
(4)根据题意设点![]() ,由题意可知四边形
,由题意可知四边形![]() 是矩形,故可得出OM×PM=6,ON×AN=6,根据
是矩形,故可得出OM×PM=6,ON×AN=6,根据![]() 可得出其面积,
可得出其面积,![]() 可求出ONOM的值,由此可得出结论.
可求出ONOM的值,由此可得出结论.
解:(1)∵正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点A(3,2),
的图象交于点A(3,2),
∴![]() ,解得
,解得![]() ,解得a=6.
,解得a=6.
∵正比例函数与反比例函数的图象均关于原点对称,
∴B(-3,-2),
∴m=-3,n=-2.
故答案为:![]() ;
;![]() ;
;![]() ;
;![]() .
.
(2)∵A(3,2)、B(-3,-2),
∴当x<-3或0<x<3时,![]() .
.
故答案为:x<-3或0<x<3.
(3)∵反比例函数的图象是一个关于原点中心对称的图形,
∴![]() ,
,![]() ,
,
∴以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形的对角线互相平分,所以以
为顶点的四边形的对角线互相平分,所以以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形一定是平行四边形.
为顶点的四边形一定是平行四边形.
∵点![]() 、
、![]() 都在第一象限,
都在第一象限,
∴![]() ,对角线
,对角线![]() 与
与![]() 不可能互相垂直,
不可能互相垂直,
∴以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形不可能是菱形,也就不可能是正方形.
为顶点的四边形不可能是菱形,也就不可能是正方形.
(4)设点![]() ,由题意可知四边形
,由题意可知四边形![]() 是矩形.
是矩形.
∵![]() 和
和![]() 都在双曲线上,
都在双曲线上,
∴![]() ,
,![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.

 口算能手系列答案
口算能手系列答案