��Ŀ����
����Ŀ��Rt��ABC�У���C��90������D��E�ֱ�����ABC��AC��BC�ϵĵ㣬��P��һ���㣮���PDA����1����PEB����2����DPE������.
(1)����P���߶�AB�ϣ���ͼ����ʾ���ҡ�����50�������1����2��________����
(2)����P�ڱ�AB���˶�����ͼ����ʾ�����������1����2֮��Ĺ�ϵΪ��____________��

(3)����P�˶�����AB���ӳ����ϣ���ͼ����ʾ�����������1����2֮���кι�ϵ�����벢˵�����ɣ�

(4)����P�˶�����ABC���⣬��ͼ����ʾ�����������1����2֮��Ĺ�ϵΪ��____________��
���𰸡�(1)140;(2) 90�㣫�Ϧ�.��3��90������2������.����4��90������1���Ϧ�.
�������������������1�������ı����ڽǺͶ����Լ��ڲ��ǵĶ��壬�ó���1+��2=��C+�����������ó����ɣ�
��2�����ã�1��������Ľ��۵ó���������1����2֮��Ĺ�ϵ���ɣ�
��3������������ǵ����ʣ��ó���1=��C+��2+��=90��+��2+����
��4�������������ڽǺͶ����Լ��ڲ��ǵ����ʿɵó���������1����2֮��Ĺ�ϵ��
�����������1���ߡ�1����2����CDP����CEP��360������C����������CDP����CEP��360����
���1����2����C��������
�ߡ�C��90����������50����
���1����2��140����
�ʴ�Ϊ��140��
��2����(1)�������C����1����2��
���1����2��90��������.
�ʴ�Ϊ����1����2��90��������.
��3����1��90������2������.�������£���ͼ����
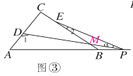
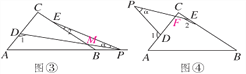
��DP��BE�Ľ���ΪM��
�ߡ�2����������DME����DME����C����1��
���1����C����2��������90������2������.
��4����ͼ����
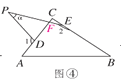
��PE��AC�Ľ���ΪF��
�ߡ�PFD����EFC��
��180������PFD��180������EFC��
�������180������1����C��180������2��
���2��90������1������.
�ʴ�Ϊ����2��90������1������