题目内容
利用我们学过的知识,可以导出下面这个形式优美的等式:a2+b2+c2-ab-bc-ac=
[(a-b)2+(b-c)2+(a-c)2],该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美;
(1)请你检验说明这个等式的正确性.
(2)若a=2011,b=2012,c=2013,你能很快求出a2+b2+c2-ab-bc-ac的值吗?
(3)若a-b=
,b-c=
,a2+b2+c2=1,求ab+bc+ac的值.
| 1 |
| 2 |
(1)请你检验说明这个等式的正确性.
(2)若a=2011,b=2012,c=2013,你能很快求出a2+b2+c2-ab-bc-ac的值吗?
(3)若a-b=
| 3 |
| 5 |
| 3 |
| 5 |
分析:(1)等式右边中括号中利用完全平方公式站那看,合并后去括号得到结果,与左边比较即可得证;
(2)根据(1)中的结论,将a,b,c的值代入右边计算即可求出值;
(3)由题意求出a-c的值,所求式子利用完全平方公式变形,将各自的值代入计算即可求出值.
(2)根据(1)中的结论,将a,b,c的值代入右边计算即可求出值;
(3)由题意求出a-c的值,所求式子利用完全平方公式变形,将各自的值代入计算即可求出值.
解答:解:(1)等式右边=
(a2-2ab+b2+b2-2bc+c2+a2-2ac+c2)=
(2a2+2b2+2c2-2ab-2bc-2ac)=a2+b2+c2-ab-bc-ac=左边,得证;
(2)当a=2011,b=2012,c=2013时,a2+b2+c2-ab-bc-ac=
[(a-b)2+(b-c)2+(a-c)2]=3;
(3)∵a-b=
,b-c=
,∴a-c=
,
∵a2+b2+c2=1,
∴ab+bc+ac=a2+b2+c2-
[(a-b)2+(b-c)2+(a-c)2]=1-
(
+
+
)=-
.
| 1 |
| 2 |
| 1 |
| 2 |
(2)当a=2011,b=2012,c=2013时,a2+b2+c2-ab-bc-ac=
| 1 |
| 2 |
(3)∵a-b=
| 3 |
| 5 |
| 3 |
| 5 |
| 6 |
| 5 |
∵a2+b2+c2=1,
∴ab+bc+ac=a2+b2+c2-
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 25 |
| 9 |
| 25 |
| 36 |
| 25 |
| 2 |
| 25 |
点评:此题考查了因式分解的应用,弄清题意是解本题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 =2009,
=2009,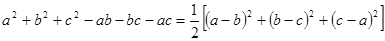 ,该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.
,该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美. =2009,
=2009, =2010,
=2010, =2011,你能很快求出
=2011,你能很快求出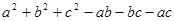 的值吗?
的值吗?