题目内容
利用我们学过的知识,可以导出下面这个形式优美的等式:a2+b2+c2-ab-bc-ac=| 1 | 2 |
(1)请你检验这个等式的正确性;
(2)若a=2005,b=2006,c=2007,你能很快求出a2+b2+c2-ab-bc-ac的值吗?
分析:(1)检验这个等式的正确性,我们可以运算逆运算,从右边向左边检验;
(2)把这三个数代入即可.
(2)把这三个数代入即可.
解答:解:(1)
[(a-b)2+(b-c)2+(c-a)2],
=
(a2-2ab+b2+b2-2bc+c2+a2-2ac+c2),
=a2+b2+c2-ab-bc-ac;
(2)a2+b2+c2-ab-bc-ac,
=
[(a-b)2+(b-c)2+(c-a)2],
=
[[(2005-2006)2+(2006-2007)2+(2007-2005)2],
=3.
| 1 |
| 2 |
=
| 1 |
| 2 |
=a2+b2+c2-ab-bc-ac;
(2)a2+b2+c2-ab-bc-ac,
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=3.
点评:本题主要考查了检验a2+b2+c2-ab-bc-ac=
[(a-b)2+(b-c)2+(c-a)2]这个公式和使用这个公式的能力.
| 1 |
| 2 |

练习册系列答案
相关题目
 =2009,
=2009,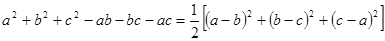 ,该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.
,该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.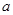 =2009,
=2009,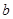 =2010,
=2010,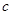 =2011,你能很快求出
=2011,你能很快求出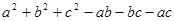 的值吗?
的值吗?