题目内容
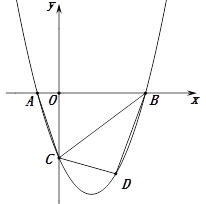
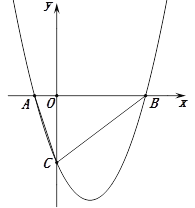
【题目】(12分)如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.

(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;
【答案】(1)y=-![]()
![]() +x+4;(2)不存在.
+x+4;(2)不存在.
【解析】
试题首先设抛物线的解析式为一般式,将点C和点A意见对称轴代入求出函数解析式;本题利用假设法来进行证明,假设存在这样的点,然后设出点F的坐标求出FH和FG的长度,然后得出面积与t的函数关系式,根据方程无解得出结论.
试题解析:(1)∵抛物线y=a![]() +bx+c(a≠0)过点C(0,4) ∴C=4①
+bx+c(a≠0)过点C(0,4) ∴C=4①
∵-![]() =1 ∴b=-2a② ∵抛物线过点A(-2,0) ∴4a-2b+c=0 ③
=1 ∴b=-2a② ∵抛物线过点A(-2,0) ∴4a-2b+c=0 ③
由①②③解得:a=-![]() ,b=1,c=4 ∴抛物线的解析式为:y=-
,b=1,c=4 ∴抛物线的解析式为:y=-![]()
![]() +x+4
+x+4
(2)不存在 假设存在满足条件的点F,如图所示,连结BF、CF、OF,过点F作FH⊥x轴于点H,FG⊥y轴于点G.设点F的坐标为(t,![]() +t+4),其中0<t<4 则FH=
+t+4),其中0<t<4 则FH=![]() +t+4 FG=t
+t+4 FG=t
∴△OBF的面积=![]() OB·FH=
OB·FH=![]() ×4×(
×4×(![]() +t+4)=-
+t+4)=-![]() +2t+8 △OFC的面积=
+2t+8 △OFC的面积=![]() OC·FG=2t
OC·FG=2t
∴四边形ABFC的面积=△AOC的面积+△OBF的面积+△OFC的面积=-![]() +4t+12
+4t+12
令-![]() +4t+12=17 即-
+4t+12=17 即-![]() +4t-5=0 △=16-20=-4<0 ∴方程无解
+4t-5=0 △=16-20=-4<0 ∴方程无解
∴不存在满足条件的点F


练习册系列答案
相关题目